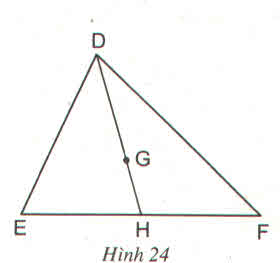
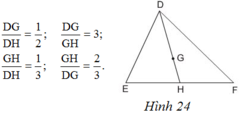
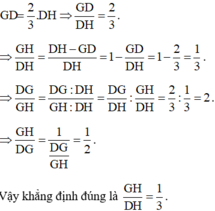cho G là trọng tâm của tam giác DEvẽ đường trung tuyến DH .trong các khẳng định sau khẳng định nao la đún A.\(\frac{DG}{DH}\frac{ }{ }\)\(=\frac{1}{2}\frac{ }{ }\)
B.\(\frac{DG}{GH}\frac{ }{ }\)=3
C.\(\frac{GH}{DH}\)\(=\frac{1}{3}\)
D.\(\frac{GH}{DG}\)\(=\frac{2}{3}\)