GIÚP EM Ý 2,3 VỚI ẠA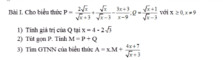
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 1:
\(\left\{{}\begin{matrix}x+y=57\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+4y=228\\4x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6y=234\\x+y=57\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=39\\x=18\end{matrix}\right.\)

1: Thay \(x=\dfrac{4-\sqrt{7}}{2}\) vào B, ta được:
\(B=\dfrac{1}{\sqrt{\dfrac{4-\sqrt{7}}{2}}+1}=1:\left(\dfrac{\sqrt{7}-1+2}{2}\right)=1\cdot\dfrac{2}{\sqrt{7}+1}=\dfrac{-1+\sqrt{7}}{3}\)

Với m=-2
Phương trình tọa độ giao điểm của (d) và (P) là:
\(2x^2=\left(-2-3\right)x+\left(-2\right)\Leftrightarrow2x^2+5x+2=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-2\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{1}{2}\\y=8\end{matrix}\right.\)
Gọi \(M\left(-\dfrac{1}{2};\dfrac{1}{2}\right),N\left(-2;8\right)\) và kẻ \(NH\perp MO\) ta có hình vẽ như sau:
Gọi phương trình đường thẳng MO là: ax+b=y
\(\left\{{}\begin{matrix}a.0+b=0\\-2a+b=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=-4\end{matrix}\right.\)
Phương trình đường thẳng MO là: -4x=y
Gọi phương trình đường thẳng NH là: ax+b=y
Để NH vuông góc với MO thì: a.a'=-1 \(\Leftrightarrow a.\left(-4\right)=-1\Leftrightarrow a=\dfrac{1}{4}\)
Ta có: \(y=\dfrac{1}{4}x+b\Leftrightarrow\dfrac{1}{2}=\dfrac{1}{4}.\dfrac{-1}{2}+b\Rightarrow b=\dfrac{5}{8}\)
Phương trình đường thẳng NH là: \(y=\dfrac{1}{4}x+\dfrac{5}{8}\)
Phương trình tọa độ giao điểm của NH và MO là: \(-4x=\dfrac{1}{4}x+\dfrac{5}{8}\Leftrightarrow x=\dfrac{-5}{34}\Rightarrow y=\dfrac{10}{17}\)
Độ dài đoạn NH là: NH= \(\sqrt{\left(-\dfrac{5}{34}--\dfrac{1}{2}\right)^2+\left(\dfrac{10}{17}-\dfrac{1}{2}\right)^2}=\dfrac{3\sqrt{17}}{34}\)
Độ dài đoạn MO là: MO=\(\sqrt{\left(-2-0\right)^2+\left(8-0\right)^2}=2\sqrt{17}\)
Diện tích tam giác OMN là: \(S=\dfrac{1}{2}NH.OM=\dfrac{1}{2}.\dfrac{3\sqrt{17}}{34}.2\sqrt{17}\)=1,5(đvdt)


Tham khảo:
Thơ của Nguyễn Đình Chiểu thường dùng để truyền bá đạo lí làm người . Khi xây dựng hình tượng Lục Vân Tiên , ông viết chàng là một người mới rời trường học , bước vào đời đầy hăm hở, muốn lập công danh, thi thố tài năng,cứu người giúp đời
-> Lục Vân Tiên là nhân vật lí tưởng thẩm mĩ của tác giả về con người
-> Ông khắc họa nhân vật theo mô típ một chàng trai tà giỏi cứu cô gái thoát khỏi tình huống hiểm nghèo : Trong thời buổi nhiễu nhương, người dân mong có người tài đức ra tay cứu nạn
-> Lục Vân Tiên còn là nhân vật lí tưởng và nơi gửi gắm ước mơ của ông


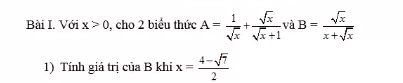



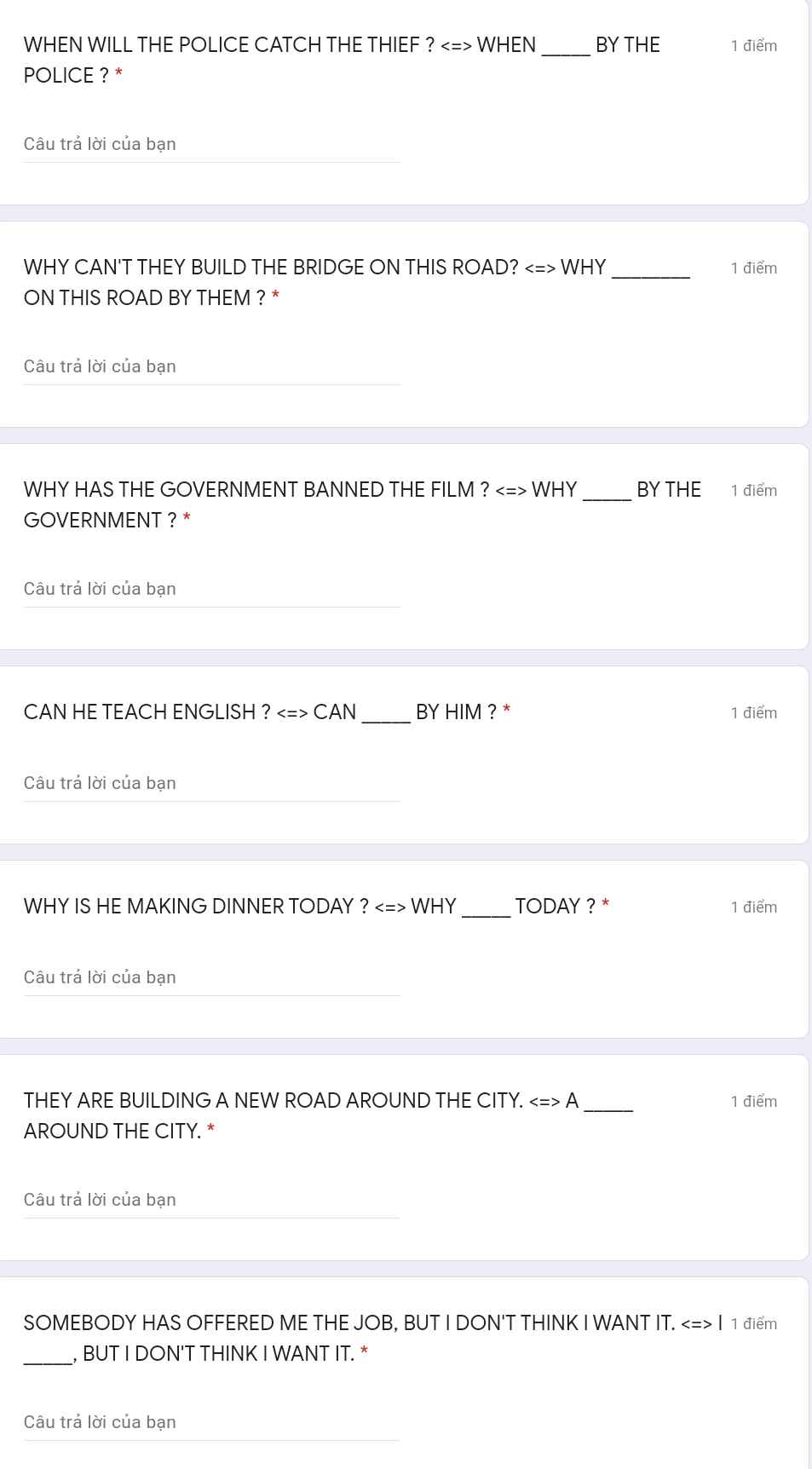 giúp em với ạa, bài này là bài tập không phải thi đâu ạa
giúp em với ạa, bài này là bài tập không phải thi đâu ạa
 giúp em với ạa
giúp em với ạa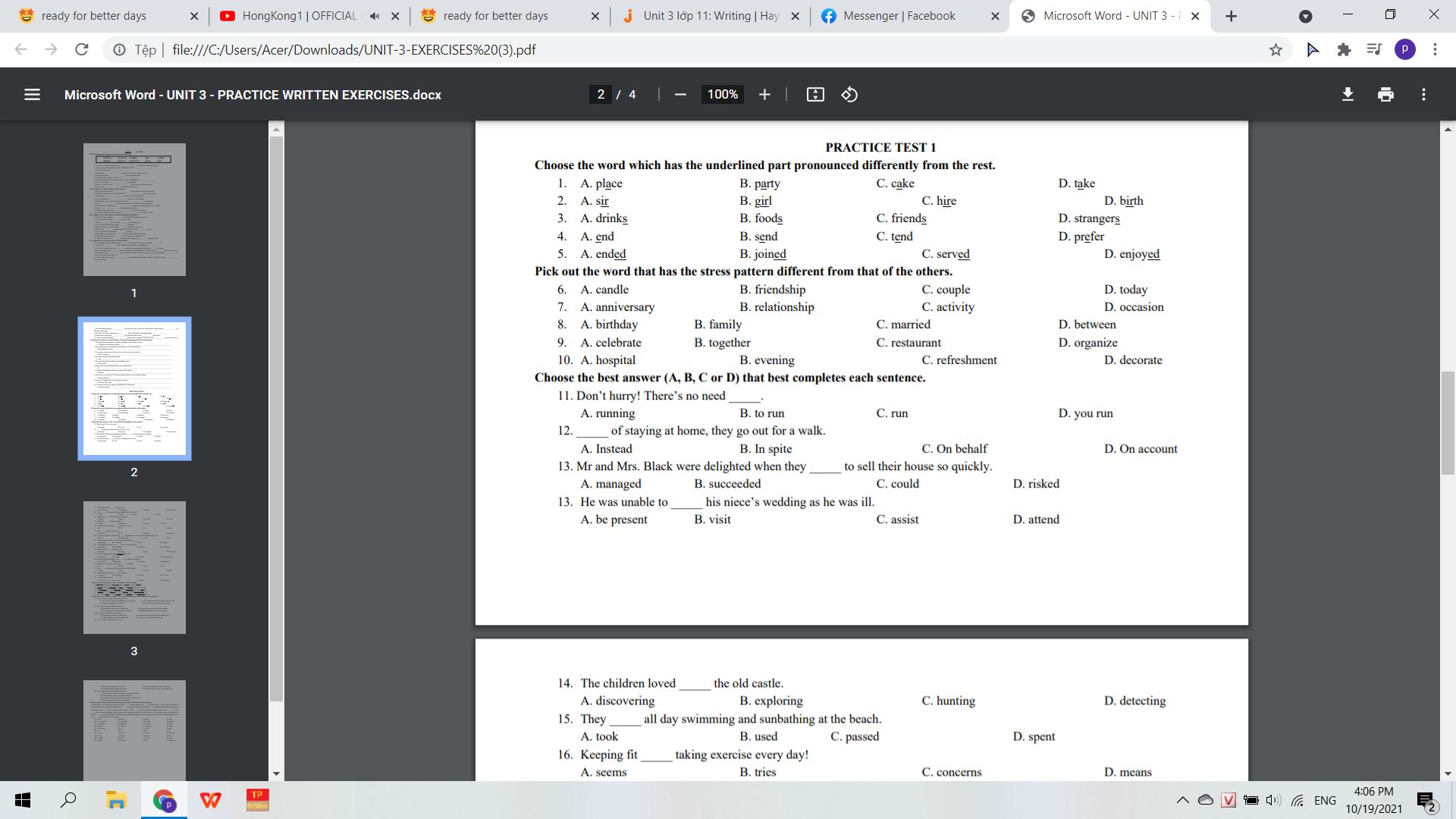
1: Thay \(x=4-2\sqrt{3}\) vào Q, ta được:
\(Q=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-3}=\dfrac{\sqrt{3}}{\sqrt{3}-4}=\dfrac{-3-4\sqrt{3}}{13}\)
2: \(P=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(M=P+Q=\dfrac{-3\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)
\(=\dfrac{-3\sqrt{x}-3+x+4\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)