a) cho A ABC vuông tại A AB (AC, AH là đường cao, đường tròn đường kính HB cắt AB tại E, đường tròn, đường kính HC cắt AC tai F Chứng minh AEHF là hình chữ nhật. b) chứng minh AE × AB = AF × AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 2 2021
a) Xét (O) có
ΔAFH nội tiếp đường tròn(A,F,H\(\in\)(O))
AH là đường kính(gt)
Do đó: ΔAFH vuông tại F(Định lí)
Xét (O) có
ΔAEH nội tiếp đường tròn(A,E,H\(\in\)(O))
Do đó: ΔAEH vuông tại E(Định lí)
Xét tứ giác AEHF có
\(\widehat{FAE}=90^0\left(\widehat{BAC}=90^0\right)\)
\(\widehat{AEH}=90^0\)(ΔAEH vuông tại E)
\(\widehat{AFH}=90^0\)(ΔAHF vuông tại F)
Do đó: AEHF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
10 tháng 4 2023
a: góc AEH=góc AFH=góc FAE=90 độ
=>AEHF là hình chữ nhật
b: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2=AE*AB
=>AE/AC=AF/AB
=>ΔAEF đồng dạng vơi ΔACB
24 tháng 10 2021
a: Xét (I) có
ΔAHC nội tiếp đường tròn
AC là đường kính
Do đó: ΔAHC vuông tại H
hay AH\(\perp\)BC
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
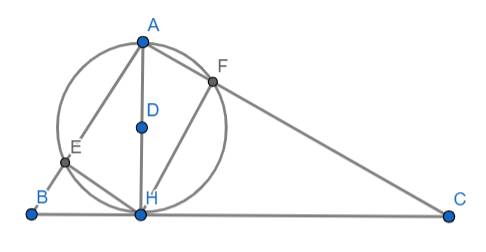
1) Ta có: \(\Delta AHF\) nội tiếp đường tròn (D) có AH là đường kính
\(\Rightarrow\widehat{AFH}=90^o\) (1)
\(\Delta AHE\) nội tiếp đường tròn (D) có AH là đường kính
\(\Rightarrow\widehat{AEH}=90^o\) (2)
Mà: \(\widehat{EAF}=90^o\left(gt\right)\) (3)
Từ (1), (2), (3) \(\Rightarrow\) Tứ giác AEHF có 3 góc vuông nên là hình chữ nhật
2) Áp dụng hệ thức lượng cho ΔABH có đường cao HE ta có:
\(AE\cdot AB=AH^2\) (4)
Áp dụng hệ thức lượng cho ΔACH có đường cao HF ta có:
\(AF\cdot AC=AH^2\) (5)
Từ (4) và (5) ta có: \(AE\cdot AB=AF\cdot AC\left(đpcm\right)\)
TM
19 tháng 4 2023
a) Ta có : \(\hat{A}=90^o\) (góc nội tiếp chắn nửa đường tròn (O), đường kính BC).
\(\hat{E}=90^o\) (góc nội tiếp chắn nửa đường tròn (I), đường kính AH).
\(\hat{F}=90^o\) (góc nội tiếp chắn nửa đường tròn (I), đường kính AH).
Suy ra, AHEF là hình chữ nhật (dấu hiệu nhận biết) (điều phải chứng minh).
b) Ta có : \(\hat{HAC}+\hat{C}=90^o\) (hai góc phụ nhau) và \(\hat{ABC}+\hat{C}=90^o\) (hai góc phụ nhau)
\(\Rightarrow\hat{HAC}=\hat{ABC}\) (điều phải chứng minh).
Mặt khác : \(\hat{AEF}=\hat{AHF}\) (hai góc nội tiếp đường tròn (I) cùng chắn cung AF).
Và : \(\left\{{}\begin{matrix}\hat{AHF}+\hat{HAC}=90^o\\\hat{C}+\hat{HAC}=90^o\end{matrix}\right.\Rightarrow\hat{AHF}=\hat{C}\). Suy ra : \(\hat{AEF}=\hat{C}\).
Lại có : \(\hat{AEF}+\hat{BEF}=180^o\) (hai góc kề bù) \(\Rightarrow\hat{C}+\hat{BEF}=180^o\).
Mà trong tứ giác BEFC, hai góc trên lại đối nhau. Do đó, tứ giác BEFC nội tiếp được một đường tròn (điều phải chứng minh).
26 tháng 11 2022
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
Xét đường tròn đương kính BH có : ^BEH = 900 ( góc nt chắn nửa đường tròn )
Xét đường tròn đường kính CH có : ^HFC = 900 ( góc nt chắn nửa đường tròn )
=> ^AEH = ^AFH = 900
Xét tứ giác AEHF có ^AEH + ^AFH = 1800
mà 2 góc này đối
Vậy tứ giác AEHF là tứ giác nt 1 đường tròn
b, Xét tam giác AHB vuông tại H, đường cao HF
Ta có : AH^2 = AE.AB (1)
Xét tam giác AHC vuông tại H, đường cao HE
Ta có : AH^2 = AF.AC (2)
Từ (1) ; (2) suy ra AE.AB = AF.AC