CMR x2+x+1 vô nghiệm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)


Chọn B và D
Phương trình B vô nghiệm vì \(5x^2+10\ge10>0\forall x\)
Phương trình C vô nghiệm vì \(x^2+6\ge6>-9\forall x\)
B và C
vì \(5x^2+10=0\Leftrightarrow5x^2=-10\Leftrightarrow x^2=-2\)(VL)
\(x^2+6=-9\Leftrightarrow x^2=-15\left(VL\right)\)

f(x)=x2+x+1=x2+\(\dfrac{1}{2}x+\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{3}{4}\)
=\(x\left(x+\dfrac{1}{2}\right)+\dfrac{1}{2}\left(x+\dfrac{1}{2}\right)+\dfrac{3}{4}\)
=\(\left(x+\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)+\dfrac{3}{4}=\left(x+\dfrac{1}{2}\right)^{^2}+\dfrac{3}{4}\)
=>f(x)≥\(\dfrac{3}{4}\)
=>đa thức trên vô nghiệm
Bài này có nhiều cách, vừa rồi là cách cơ bản, còn nếu bạn muốn nâng cao chút thì có thể dùng cách này nha:
Xét x≥0 thì x+1>0
x(x+1)≥0=>x(x+1)+1>0 =>x2+x+1>0 (1)
Xét -1<x<0 thì x+1≤0. Ta lại có x2≥0 nên x2+x+1 >0 (2)
Xét x≤-1 thì x<0 và x+1≤0. Do đó
x(x+1) ≥0=>x(x+1) +1>0=>x2+x+1>0 (3)
Từ (1), (2), (3)=> đa thức f(x) vô nghiệm


Có P(x)=3x^4+x^2+1/4
Vì 3x^4 \(\ge\) 0 Với mọi x
x^2 \(\ge\) 0 Với mọi x
nên 3x^4+x^2 \(\ge\) 0 với mọi x
=>3x^4+x^2+1/4 \(\ge\) 0+1/4 >0 với mọi x
=>P(x) > với mọi x
Vậy P(x) vô nghiệm


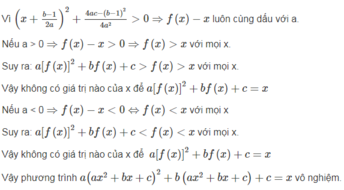
Ta có x² + x + 1
= x² + x + 4/4
= x² + x + 1/4 + 3/4
= (x² + x + 1/4) + 3/4
= (x² + 2.x.(1/2) + (1/2)² ) + 3/4
= (x + 1/2)² + 3/4
Do (x + 1/2) ≥ 0 ∀ x ∈ R
=> (x + 1/2)² + 3/4 ≥ 3/4 > 0 ∀ x ∈ R
=> x² + x + 1 > 0 ∀ x ∈ R
=> đpcm
Ta có x² + x + 1
= x² + x + 4/4
= x² + x + 1/4 + 3/4
= (x² + x + 1/4) + 3/4
= (x² + 2.x.(1/2) + (1/2)² ) + 3/4
= (x + 1/2)² + 3/4
Do (x + 1/2) ≥ 0 ∀ x ∈ R
=> (x + 1/2)² + 3/4 ≥ 3/4 > 0 ∀ x ∈ R
=> x² + x + 1 > 0 ∀ x ∈ R
=> đpcm