ΔMKN có góc K=90 độ,theo định lí Pitago ta có..?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 6 2018
ap dung dinh li pi ta go cua tam giac vuong ABC
\(\Rightarrow BC^2=\text{A}B^2+\text{A}C^2\)
\(\Rightarrow BC^2=2^2+5^2\)
\(\Rightarrow BC^2=14\)
VAY \(BC=\sqrt{14}\) BN OI KO DUNG DINH LI PI TA GO LAM THE NAO..HAY BN VIẾT THIẾU ĐỀ
…………………………………………………………………………..
CM
24 tháng 12 2018
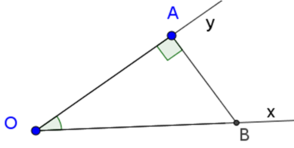
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
CM
4 tháng 5 2018
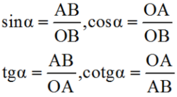
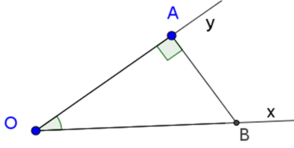
Dựng góc nhọn ∠xOy = α tùy ý.
Trên tia Ox lấy điểm B bất kì, kẻ BA ⊥ Oy (A ∈ Oy)
Theo định nghĩa tỉ số lượng giác của góc nhọn, ta có:
b) Áp dụng định lí pitago trong tam giác vuông OAB có:
O B 2 = O A 2 + A B 2
Từ đó ta có:
HP
20 tháng 1 2016
Xét tam giác ABC có A=90 độ=>tam giác ABC vuông ở A
áp dụng Py-ta-go :
BC2=AB2+AC2
=>102=AB2+(căn 75)2
=>100=AB2+75
=>AB2=25=>AB=5(cm)
câu b tự lm nhé bn,dễ lắm
20 tháng 1 2016
Xét tam giác ABC có A=90 độ
=>tam giác ABC vuông ở A ( theo định lí Pytago đảo)
Theo định lí Py-ta-go ta có:
BC2=AB2+AC2
=>102=AB2+(\(\sqrt{75}\))2
=>100=AB2+75
=>AB2=25
=>AB=5(cm)
b)Ta có: AB=5cm (chứng minh trên)
BC=10cm (GT)
=>AB= 1/2 BC
=>Tam giác ABC là tam giác nửa đều
=> góc B=60o và góc C=30o (tính chất tam giác nửa đều)
18 tháng 5 2022
a: Do AC > A'C' nên lấy được điểm C1 trên cạnh AC sao cho AC1=A′C′.
Ta có ΔABC1=ΔA'B'C'
Suy ra B′C′=BC1
Mặt khác hai đường xiên BC và BC1 kẻ từ B đến đường thẳng AC lần lượt có hình chiếu trên AC là AC và AC1.
Vì AC > AC1 nên BC > BC1.
Suy ra BC > B'C'.
b:
-Giả sử AC<A'C'.
Khi đó theo chứng minh câu a) ta có BC < B'C'. Điều này không đúng với giả thiết BC > B'C'.
Giả sử AC=A'C'. Khi đó ta có ΔABC=ΔA'B'C' (c.g.c).
Suy ra BC=B'C'.
Điều này cũng không đúng với giả thiết BC>B'C'. Vậy ta phải có AC>A'C'.
\(KM^2+KN^2=MN^2\)
ta có MK2+NK2=MN2