Có ai đó giúp mình với mình cảm ơn (giải thích chi tiết)
So sánh:
K
Khách
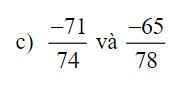
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
1
HN
13 tháng 10 2021
Ta có: (u.v)' = u'.v + u.v'
\(Q=80K^{\dfrac{1}{3}}\left(100-K\right)^{\dfrac{1}{2}}\)
\(Q'=80.\left(K^{\dfrac{1}{3}}\right)'.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\left(\left(100-K\right)^{\dfrac{1}{2}}\right)'\)= \(80.\dfrac{1}{3}.K^{-\dfrac{2}{3}}.\left(100-K\right)^{\dfrac{1}{2}}+80.K^{\dfrac{1}{3}}.\dfrac{1}{2}.\left(100-K\right)^{-\dfrac{1}{2}}.\left(-1\right)\) = \(80.\left(\dfrac{\left(100-K\right)^{\dfrac{1}{2}}}{3K^{\dfrac{2}{3}}}-\dfrac{K^{\dfrac{1}{3}}}{2\left(100-K\right)^{\dfrac{1}{2}}}\right)\)= \(80.\left(\dfrac{2\left(100-K\right)^{\dfrac{1}{2}}\left(100-K\right)^{\dfrac{1}{2}}-3K^{\dfrac{2}{3}}K^{\dfrac{1}{3}}}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{2\left(100-K\right)-3K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(80.\left(\dfrac{200-5K}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\right)\) = \(\dfrac{400\left(40-K\right)}{6K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\) = \(\dfrac{200\left(40-K\right)}{3K^{\dfrac{2}{3}}\left(100-K\right)^{\dfrac{1}{2}}}\).
N
0
PT
0
PT
0
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
TL
0
PT
1
23 tháng 4 2017
Ta có :
\(\frac{1}{12}=\frac{1}{12}\)
\(\frac{1}{13}< \frac{1}{12}\)
\(\frac{1}{14}< \frac{1}{12}\)
\(........\)
\(\frac{1}{17}< \frac{1}{12}\)
Cộng vế với vế ta có :
\(\frac{1}{12}+\frac{1}{13}+....+\frac{1}{17}< \frac{1}{12}+\frac{1}{12}+...+\frac{1}{12}\)(có 6 số \(\frac{1}{12}\))\(=\frac{6}{12}=\frac{1}{2}\)
Vậy \(\frac{1}{12}+\frac{1}{13}+\frac{1}{14}+....+\frac{1}{17}< \frac{1}{2}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 8 2023
Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)
4 tháng 8 2017
\(\frac{123}{124}\) < \(\frac{124124}{125125}\)
Bạn chỉ cần lấy tử chia cho mẫu là ra
c)Em quy đồng lên và có mẫu chung là 5772 nhé
=>-5538/5772 và -4810/5772
=>-4810>-5538
=>-65/78>-71/74 nhé
ok a