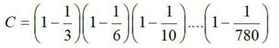
Có anh chị hay thầy cô nào giúp em với ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



- Không có thời gian nhất định đâu ! Khi nào thầy cô giáo online thì mới tick được
vế vấn đề này pn ko cần phải lo! Pn cứ tl các câu hoj đi. Khi nào admin onl thấy câu tl của pn đúng, ko copy bài của pn khác thì sẽ ticks liền


PTBĐ chính: thuyết minh.
(Bạn làm bài có thể nhìn mẹo chỗ ngoặc nếu phân vân, đã là "theo tài liệu khoa học" tức là cung cấp thông tin đó bạn).

Câu 1: Nguyên nhân chính giúp thực vật C4 và CAM không có hiện tượng hô hấp sáng là gì?
Đáp án: Do ở 2 nhóm thực vật này có hệ enzim phosphoenolpyruvat cacboxylaz với khả năng cố định CO2 trong điều kiện hàm lượng CO2 thấp,tạo acid malic là nguồn dự trữ CO2 cung cấp cho các tế bào bao quanh bó mạch,giúp hoạt tính carboxyl của enzim RibDPcarboxilaz luôn thắng thế hoạt tính ôxy hóa nên ngăn chận được hiện tượng quang hô hấp.
Câu 2: Tại sao đều không có hiện tượng hô hấp sáng,nhưng thực vật C4 có năng suất cao còn thực vật CAM lại có năng suất thấp?
Đáp án: Thực vật CAM sử dụng sản phẩm cuối cùng của quá trình quang hợp tích lũy dưới dạng tinh bột làm nguyên liệu tái tạo chất nhận CO2 của chu trình CAM,điều này làm giảm chất hữu cơ tích lũy trong cây à năng suất thấp.

Đặt \(\int f\left(x\right)dx=F\left(x\right)\Rightarrow\int\limits^{17}_1f\left(x\right)dx=F\left(17\right)-F\left(1\right)\)
Từ giả thiết:
\(2x.f\left(x^2+1\right)+\dfrac{f\left(\sqrt{x}\right)}{2\sqrt{x}}=2lnx\)
Lấy nguyên hàm 2 vế:
\(F\left(x^2+1\right)+F\left(\sqrt{x}\right)=2xlnx-2x+C\)
Thay \(x=4\):
\(F\left(17\right)+F\left(2\right)=16ln2-8+C\) (1)
Thay \(x=1\):
\(F\left(2\right)+F\left(1\right)=-2+C\) (2)
Trừ vế cho vế (1) cho (2):
\(F\left(17\right)-F\left(1\right)=16ln2-6\)
Vậy \(\int\limits^{17}_1f\left(x\right)dx=16ln2-6\)
\(C=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}...\dfrac{779}{780}=\dfrac{2.2}{3.2}.\dfrac{5.2}{6.2}.\dfrac{9.2}{10.2}...\dfrac{779.2}{780.2}\)
\(=\dfrac{4}{6}.\dfrac{10}{12}.\dfrac{18}{20}...\dfrac{1558}{1560}=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{38.41}{39.40}\)
\(=\dfrac{1.2.3...38}{2.3.4...39}.\dfrac{4.5.6...41}{3.4.5...40}=\dfrac{1}{39}.\dfrac{41}{3}=\dfrac{41}{117}\)
\(C=\left(1-\dfrac{2}{6}\right)\left(1-\dfrac{2}{12}\right)\left(1-\dfrac{2}{20}\right)...\left(1-\dfrac{2}{1560}\right)\)
\(=\left(1-\dfrac{2}{2.3}\right)\left(1-\dfrac{2}{3.4}\right)\left(1-\dfrac{2}{4.5}\right)...\left(1-\dfrac{2}{39.40}\right)\)
Ta có: \(1-\dfrac{2}{n\left(n+1\right)}=\dfrac{n\left(n+1\right)-2}{n\left(n+1\right)}=\dfrac{n^2+n-2}{n\left(n+1\right)}=\dfrac{\left(n-1\right)\left(n+2\right)}{n\left(n+1\right)}\)
Do đó:
\(C=\dfrac{1.4}{2.3}.\dfrac{2.5}{3.4}.\dfrac{3.6}{4.5}...\dfrac{38.41}{39.40}\)
\(=\dfrac{1.2.3...38}{2.3.4...39}.\dfrac{4.5.6...41}{3.4.5...40}=\dfrac{1}{39}.\dfrac{41}{3}=\dfrac{41}{117}\)