Cho hình thang ABCD (AB//CD) biết DC=2AB, I là trung điểm của DC,nối AI với BI. Xác định các cặp tam giác đồng dạng có trong hình(có giải thích)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 8 2017
Học sinh sử dụng tính chất các tam giác bằng nhau thì đồng dạng với nhau để chứng minh
TQ
1 tháng 2 2018
Xét tứ giác ABED có:
AB//DE;AB=DE
=>ABED là hình bình hành ( một cặp cạnh vừa song song vừa bằng nhau)
nên AD=BE
Xét tam giác EDA và tam giác ABE có:
AB=DE (gt)
AE là cạnh chung
AD=BE ( vừa chứng minh)
=>tam giác EDA =tam giác ABE
<=>tam giác EDA đồng dạng với tam giác ABE (1)
Xét tứ giác ABCE có:
AB//EC;AB=EC
=>ABCE là hình bình hành (một cặp cạnh vừa song song vừa bằng nhau
=>AE=BC
Xét tam giác ABE và tam giác CEB có:
AB=EC(gt)
BE là cạnh chung
AE=BC (vừa chứng minh)
=>tam giác ABE=tam giác CEB
<=>tam giác ABE đồng dạng với tam giác CEB (2)
từ (1) và (2)
=>tam giác EDA đồng dạng với tam giác ABE và đồng dang với tam giác CEB.
Ai biết cách vẽ kí hiệu đồng dạng không chỉ mình cách vẽ với cảm mơn bạn nhiều.
5 tháng 10 2022
Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
10 tháng 2 2022
a: Xét tứ giác ABPD có
AB//PD
AB=PD
Do đó: ABPD là hình bình hành
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình
=>MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình
=>QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
b: Để MNPQ là hình thoi thì MN=MQ
hay AC=BD
CM
21 tháng 3 2019
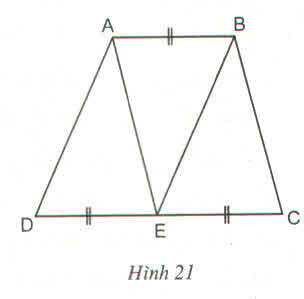
Vì CD = 2AB (gt) nên AB = 1/2 CD
Vì E là trung điểm của CD nên DE = EC = 1/2 CD
Suy ra: AB = DE = EC
Hình thang ABCD có đáy AB = EC nên hai cạnh bên AE và BC song song với nhau
Xét △ AEB và △ CBE, ta có:
∠ (ABE) = ∠ ( BEC)(So le trong)
∠ (AEB) = ∠ (EBC) (so le trong)
BE cạnh chung
⇒ △ AEB = △ CBE (g.c.g) (1)
Hình thang ABCE có đáy AB = DE nên hai cạnh bên AD và BE song song với nhau
Xét △ AEB và △ EAD, ta có:
∠ (BAE) = ∠ (AED)(so le trong)
∠ (AEB) = ∠ (EAD) (so le trong)
AE cạnh chung
⇒ △ AEB = △ EAD(g.c.g) (2)
Từ (1) và (2) suy ra: ΔAEB = ΔCBE = ΔEAD
Vậy ba tam giác △ AEB; △ CBE và △ EAD đôi một đồng dạng
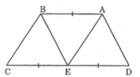
I là trung điểm của DC (gt).
\(\Rightarrow DC=2DI=2IC.\)
Mà \(DC=2AB\left(gt\right).\)
\(\Rightarrow AB=DI=IC.\)
Xét tứ giác ABDI:
\(AB//DI\left(AB//DC\right).\\ AB=DI\left(cmt\right).\)
\(\Rightarrow\) Tứ giác ABDI là hình bình hành (dhnb).
\(\Rightarrow\widehat{ABI}=\widehat{ADI}\) (Tính chất hình bình hành).
Xét tứ giác ABCI:
\(AB//IC\left(AB//DC\right).\\ AB=IC\left(cmt\right).\)
\(\Rightarrow\) Tứ giác ABCI là hình bình hành (dhnb).
\(\Rightarrow\widehat{BAI}=\widehat{BCI}\) (Tính chất hình bình hành).
Xét \(\Delta ABI\) và \(\Delta IDA:\)
\(\widehat{ABI}=\widehat{IDA}\left(cmt\right).\\ \widehat{IAB}=\widehat{AID}\left(AB//DC\right).\\ \Rightarrow\Delta ABI\sim\Delta IDA\left(g-g\right).\left(1\right)\)
Xét \(\Delta ABI\) và \(\Delta CIB:\)
\(\widehat{BAI}=\widehat{ICB}\left(cmt\right).\\ \widehat{ABI}=\widehat{CIB}\left(AB//DC\right).\\ \Rightarrow\Delta ABI\sim\Delta CIB\left(g-g\right).\left(2\right)\)
Từ \(\left(1\right);\left(2\right).\Rightarrow\) \(\Delta IDA\) \(\sim\Delta CIB.\)
Vậy các cặp tam giác đồng dạng có trong hình là:
\(\Delta ABI\sim\Delta IDA;\) \(\Delta ABI\sim\Delta CIB;\) \(\Delta IDA\) \(\sim\Delta CIB.\)