Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA=OB=2OC. gọi M là trung điểm của BC, tính cosin góc của OM và AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 3 2021
Bạn tự vẽ hình nhé!
Giả sử: OC = a ⇒ OB = 3/2a và OA = 3a
Xét tam giác OAB vuông tại O có: \(AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}a\)
\(\Rightarrow AM=BM=OM=\dfrac{1}{2}AB=\dfrac{3\sqrt{5}}{4}a\)
Xét tam giác OMA, có:
\(\cos\widehat{AOM}=\dfrac{OM^2+OA^2-AM^2}{2OM.OA}=\dfrac{OA}{2OM}=\dfrac{2\sqrt{5}}{5}\)
Xét tam giác OMB, có:
\(\cos\widehat{BOM}=\dfrac{OM^2+OB^2-BM^2}{2OM.OB}=\dfrac{OB}{2OM}=\dfrac{\sqrt{5}}{4}\)
Ta có: \(\overrightarrow{OM}.\overrightarrow{AB}=\overrightarrow{OM}\left(\overrightarrow{OB}-\overrightarrow{OA}\right)=\overrightarrow{OM}.\overrightarrow{OB}-\overrightarrow{OM}.\overrightarrow{OA}\)
\(=\dfrac{3\sqrt{5}}{4}a.\dfrac{3}{2}a.\dfrac{2\sqrt{5}}{5}-\dfrac{3\sqrt{5}}{4}a.3a.\dfrac{\sqrt{5}}{4}=\dfrac{-9}{16}a^2\)
\(\Rightarrow\cos\widehat{\left(\overrightarrow{OM},\overrightarrow{AB}\right)=\dfrac{\overrightarrow{OM}.\overrightarrow{AB}}{OM.AB}=-\dfrac{1}{10}}\)
\(\Rightarrow cos\left(OM,AB\right)=\dfrac{1}{10}\)
19 tháng 3 2021
Hicc, ở phần tính cos BOM mình bấm máy nhầm, bạn tự bấm lại nhé. :((((
Còn cả đoạn thay cos AOM và cos BOM vào tích vô hướng cũng bị lộn giữa 2 góc á.
Kết quả ra là 3/5 nhé!
Tự dưng giờ xem lại mới nhận ra lỗi sai nghiêm trọng này. Xin lỗi bạn nhé!
CM
16 tháng 10 2017
Gọi N là trung điểm của AC ⇒ M N / / A B , Vậy
( OM,AB ) = ( OM,MN ) = OMN
Cho OA = OB = OC = 1. Ta có.
M N = A B 2 = 2 2 O M = B C 2 = 2 2 O N = A C 2 = 2 2
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Đáp án cần chọn là C
CM
7 tháng 9 2018
Đáp án C
Cách 1.
Gọi N là trung điểm của AC ⇒ M N / / A B
Cho OA =OB =OC =1. Ta có.
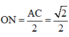
Vậy ∆ O M N là tam giác đều và O M N = 60 o
Cách 2. Dùng pp tọa độ hóa và công thức
CM
30 tháng 5 2017
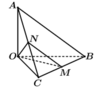
Đặt
O
A
=
O
B
=
O
C
= a suy ra 
Gọi N là trung điểm AC, ta có MN//AB. Khi đó 
Trong tam giác OMN có 
nên OMN là tam giác đều
Chọn C.
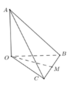
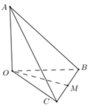
Đặt \(OA=OB=2OC=2a\)
\(\Rightarrow BC=\sqrt{OB^2+OC^2}=a\sqrt{5}\) \(\Rightarrow OM=\dfrac{1}{2}BC=\dfrac{a\sqrt{5}}{2}\)
Qua B kẻ đường thẳng song song OM cắt OC kéo dài tại D
\(\Rightarrow OM\) là đường trung bình tam giác BCD \(\Rightarrow BD=2OM=a\sqrt{5}\)
\(OM||BD\Rightarrow\left(OM;AB\right)=\left(BD;AB\right)=\widehat{ABD}\)
\(AB=\sqrt{OA^2+OB^2}=2a\sqrt{2}\)
\(AD=\sqrt{OA^2+OD^2}=\sqrt{OA^2+OC^2}=a\sqrt{5}\)
\(\Rightarrow cos\widehat{ABD}=\dfrac{AB^2+BD^2-AD^2}{2AB.BD}=\dfrac{\sqrt{10}}{5}\)