Giusp em với ạ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Với \(m=-1\) pt trở thành: \(x^2+4x-2=0\)
\(\Delta'=4+2=6>0\) nên pt có 2 nghiệm pb:
\(x_1=-2+\sqrt{6}\) ; \(x_2=-2-\sqrt{6}\)
b.
\(\Delta'=\left(m-1\right)^2-\left(m^2-3\right)=-2m+4\ge0\Rightarrow m\le2\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m-1\right)\\x_1x_2=m^2-3\end{matrix}\right.\)
\(x_1\left(x_1-x_2\right)+x_2^2=33\)
\(\Leftrightarrow x_1^2+x_2^2-x_1x_2=33\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-3x_1x_2=33\)
\(\Leftrightarrow4\left(m-1\right)^2-3\left(m^2-3\right)=33\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10>2\left(loại\right)\\m=-2\end{matrix}\right.\)

Bài 4:
Điện trở tương đương: \(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{40.60}{40+60}=24\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=I.R_{tđ}=0,5.24=12\left(V\right)\)
Cường độ dòng điện qua mỗi điện trở:
\(\left\{{}\begin{matrix}I_1=\dfrac{U_1}{R_1}=\dfrac{12}{40}=0,3\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{12}{60}=0,2\left(A\right)\end{matrix}\right.\)
\(P=U.I=12.0,5=6\left(W\right)\)
\(A=P.t=6.1.60.60=21600\left(J\right)\)
Bài 5:
Điện trở tương đương của cả mạch: \(R_{tđ}=\dfrac{R_1.R_2}{R_1+R_2}=\dfrac{3.6}{3+6}=2\left(\Omega\right)\)
Do mắc song song nên \(U=U_1=U_2=18V\)
Cường độ dòng điện qua mỗi điện trở và cả mạch:
\(\left\{{}\begin{matrix}I=\dfrac{U}{R_{tđ}}=\dfrac{18}{2}=9\left(A\right)\\I_1=\dfrac{U_1}{R_1}=\dfrac{18}{3}=6\left(A\right)\\I_2=\dfrac{U_2}{R_2}=\dfrac{18}{6}=3\left(A\right)\end{matrix}\right.\)
Tiết diện của dây: \(R_2=\rho_2.\dfrac{l_2}{S_2}\Rightarrow S_2=\dfrac{\rho_2.l_2}{R_2}=\dfrac{1,6.10^{-6}.10}{6}\approx2,67.10^{-6}\left(m^2\right)\)


a.
Với \(m=3\) pt trở thành: \(2x^2+5x+2=0\)
\(\Delta=5^2-4.2.2=9>0\) nên pt có 2 nghiệm phân biệt:
\(x_1=\dfrac{-5+\sqrt{9}}{2.2}=-\dfrac{1}{2}\)
\(x_2=\dfrac{-5-\sqrt{9}}{2.2}=-2\)
b.
\(\Delta=\left(2m-1\right)^2-8\left(m-1\right)=4m^2-12m+9=\left(2m-3\right)^2\ge0;\forall m\)
Phương trình luôn có 2 nghiệm với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{2m-1}{2}\\x_1x_2=\dfrac{m-1}{2}\end{matrix}\right.\)
\(4x_1^2+2x_1x_2+4x_2^2=1\)
\(\Leftrightarrow4\left(x_1^2+2x_1x_2+x_2^2\right)-6x_1x_2=1\)
\(\Leftrightarrow4\left(x_1+x_2\right)^2-6x_1x_2=1\)
\(\Leftrightarrow\left(2m-1\right)^2-3\left(m-1\right)=1\)
\(\Leftrightarrow4m^2-7m+3=0\Rightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{3}{4}\end{matrix}\right.\)

Ptr hoành độ của `(P)` và `(d)` là:
`x^2=-5x-3m+1`
`<=>x^2+5x+3m-1=0` `(1)`
Để `(P)` cắt `(d)` tại `2` điểm phân biệt thì ptr `(1)` có `2` nghiệm phân biệt
`=>\Delta > 0`
`<=>5^2-4(3m-1) > 0`
`<=>25-12m+4 > 0`
`<=>m < 29/12`
`=>` Áp dụng Viét có: `{(x_1+x_2=-b/a=-5),(x_1.x_2=c/a=3m-1):}`
Ta có: `[x_1 ^2]/[x_2]-[x_2 ^2]/[x_1]+3=75/[x_1.x_2]`
`<=>[x_1 ^3-x_2 ^3]/[x_1.x_2]+[3x_1.x_2]/[x_1.x_2]=75/[x_1.x_2]`
`=>(x_1-x_2)(x_1 ^2+x_1.x_2+x_2 ^2)+3x_1.x_2=75`
`<=>(x_1-x_2)[(x_1+x_2)^2-x_1.x_2]+3x_1.x_2=75`
`<=>(x_1-x_2)[(-5)^2-3m+1]+3(3m-1)=75`
`<=>(x_1-x_2)(26-3m)=78-9m`
`<=>x_1-x_2=[3(26-3m)]/[26-3m]`
`<=>x_1-x_2=3`
Kết hợp với `x_1+x_2=-5`
Giải hệ `=>{(x_1=-1),(x_2=-4):}`
Thay vào `x_1.x_2=3m-1` có:
`-1.(-4)=3m-1`
`<=>m=5/3` (t/m)

\(b,\dfrac{\sqrt{12}-\sqrt{6}}{\sqrt{30}-\sqrt{15}}=\dfrac{\sqrt{6}\left(\sqrt{2}-1\right)}{\sqrt{15}\left(\sqrt{2}-1\right)}=\dfrac{\sqrt{6}}{\sqrt{15}}=\dfrac{\sqrt{2}}{\sqrt{5}}\)
\(d,\dfrac{ab-bc}{\sqrt{ab}-\sqrt{bc}}=\dfrac{\left(\sqrt{ab}-\sqrt{bc}\right)\left(\sqrt{ab}+\sqrt{bc}\right)}{\left(\sqrt{ab}-\sqrt{bc}\right)}=\sqrt{ab}+\sqrt{bc}=\sqrt{b}\left(\sqrt{a}+\sqrt{c}\right)\)
\(e,\left(a\sqrt{\dfrac{a}{b}+2\sqrt{ab}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\left(\sqrt{\dfrac{a}{b}+\dfrac{2b.\sqrt{ab}}{b}}+b\sqrt{\dfrac{a}{b}}\right)\sqrt{ab}\)
\(=a\sqrt{a}\sqrt{a+2b\sqrt{ab}}+b\sqrt{a^2}\)
\(=a\sqrt{a^2+2ab\sqrt{ab}}+ab\)
\(=a\left(\sqrt{a^2+2ab\sqrt{ab}}+b\right)\)
\(f,\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1+a\sqrt{a}}{1+\sqrt{a}}-\sqrt{a}\right)\)
\(=\left(a+\sqrt{a}+1+\sqrt{a}\right)\left(a-\sqrt{a}+1-\sqrt{a}\right)\)
\(=\left(a+2\sqrt{a}+1\right)\left(a-2\sqrt{a}+1\right)\)
\(=\left(\sqrt{a}+1\right)^2\left(\sqrt{a}-1\right)^2\)
\(=\left(a-1\right)^2=a^2-2a+1\)

a: Thay x=2 và y=0 vào (d), ta được:
-n+3+4=0
=>1-n=0
hay n=1
b: Phương trình hoành độ giao điểm là:
\(x^2-2x+n-3=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot\left(n-3\right)=-4n+12+4=-4n+16\)
Để phương trình có hai nghiệm phân biệt thì -4n+16>0
hay n<4

ý nghĩa cuộc chiến tranh thế giới thứ hai? | Yahoo Hỏi & Đáp
“Kẻ gieo gió phải gặt bão" - chiến tranh kết thúc với sự sụp đổ hoàn toàn của chủ nghĩa phát xít Đức, I-ta-li-a. Nhật Bản. Tuy nhiên, toàn nhân loại đã phải hứng chịu những hậu quả thảm khốc của chiến tranh.
Chiến tranh thế giới thứ hai là cuộc chiến tranh lớn nhất, khốc liệt nhất và tàn phá nặng nề nhất trong lịch sử loài người : 60 triệu người chết, 90 triệu người bị tàn tật, thiệt hại về vật chất gấp 10 lần so với Chiến tranh thế giới thứ nhất, bằng tất cả các cuộc chiến tranh trong 1000 năm trước đó cộng lại.
Chiến tranh kết thúc đã dẫn đến những biến đổi căn bản của tình hình thế giới.

\(\left(x^2+6x+8\right)\left(x^2+14x+48\right)+16\)
\(=\left(x+2\right)\left(x+4\right)\left(x+6\right)\left(x+8\right)+16\)
\(=\left(x^2+10x+16\right)\left(x^2+10x+24\right)+16\)
\(=\left(x^2+10x\right)^2+40\left(x^2+10x\right)+400\)
\(=\left(x^2+10x+20\right)^2\)
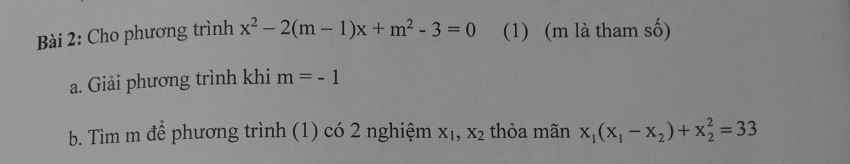


 đây nha em
đây nha em

 Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.
Giusp em với mọi người ạ. Rút gọn câu d, e, f, b giúp em với ạ, Em cảm ơn nhiều lắm.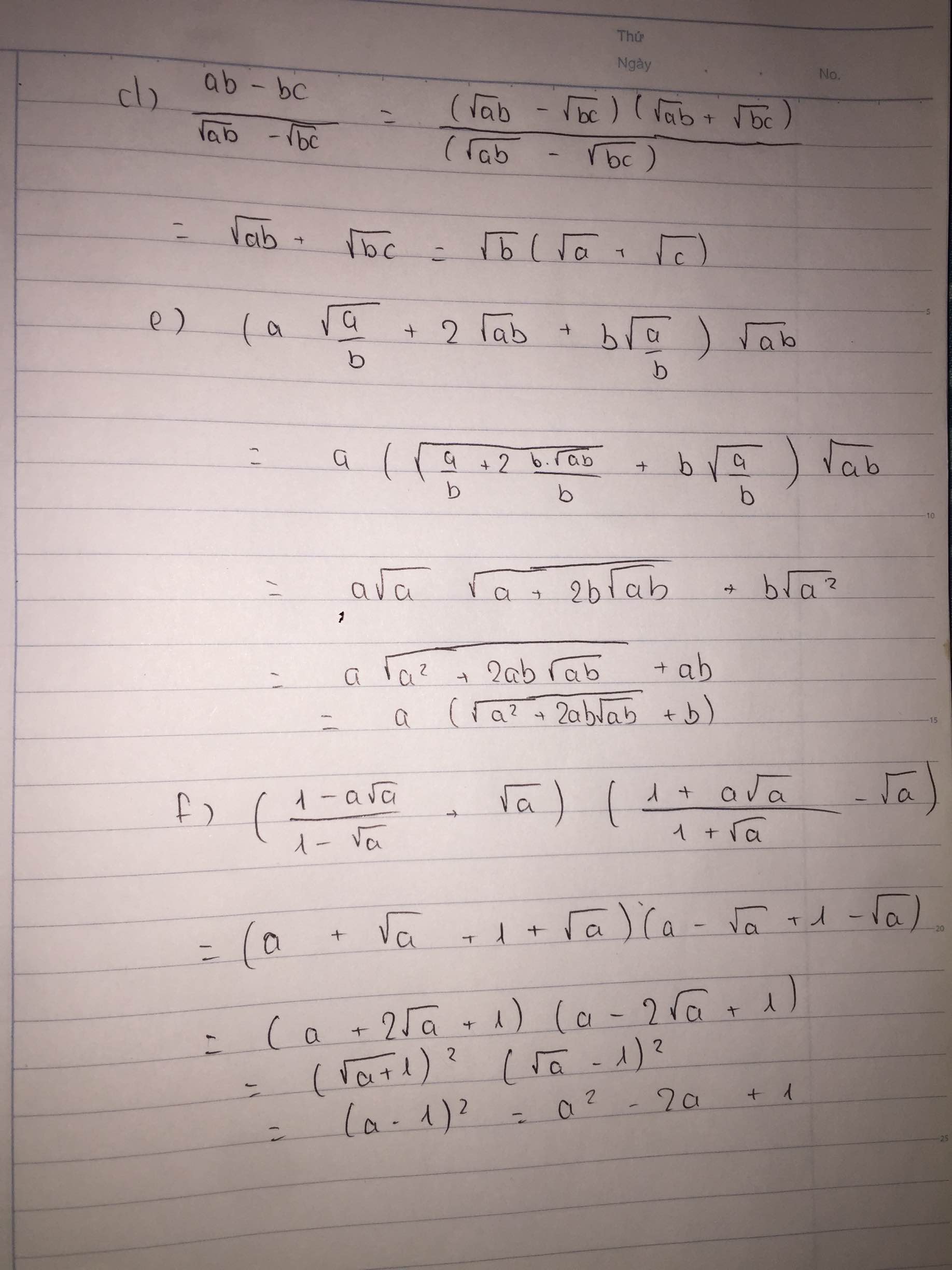
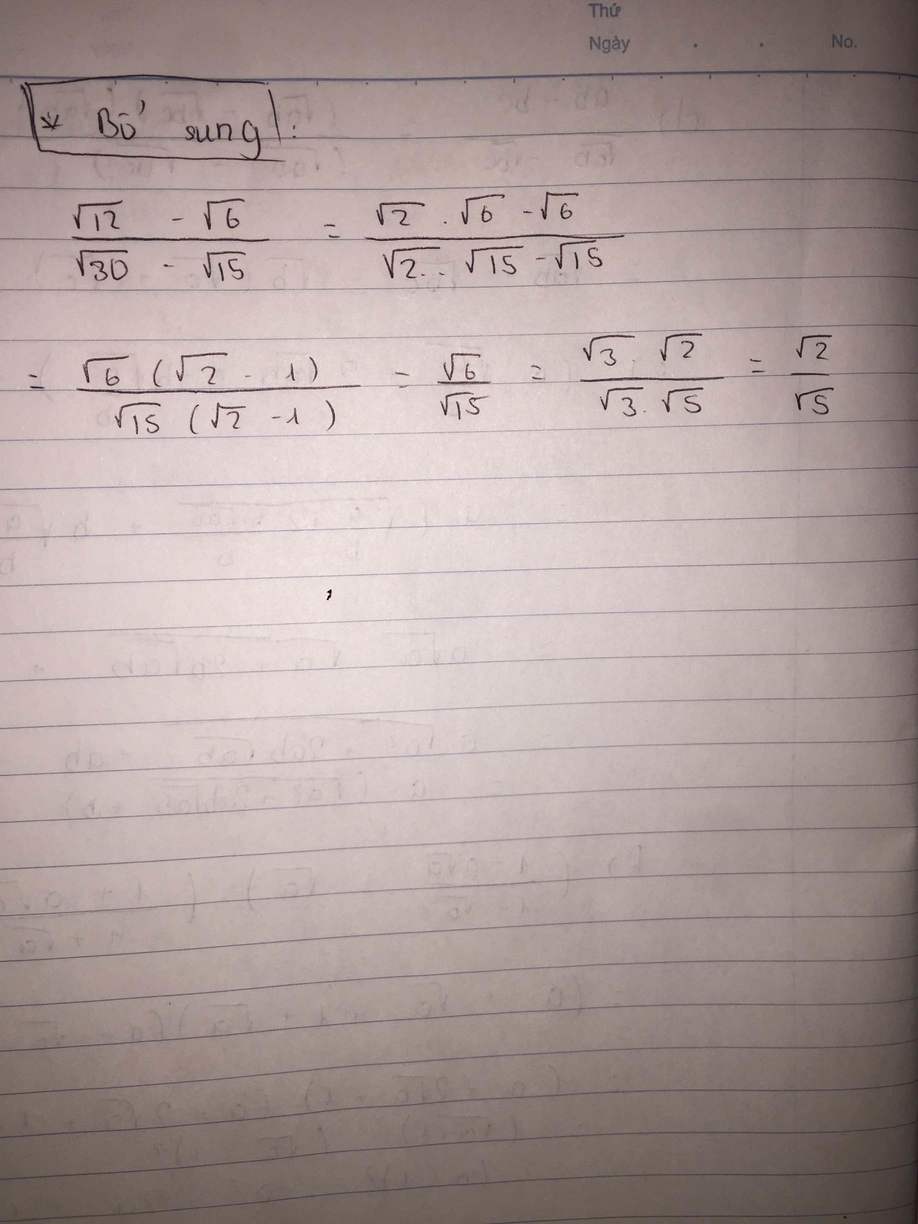

a) Với x>0,x\(\ne\)9
\(Q=\left(\dfrac{1}{x-3\sqrt{x}}+\dfrac{1}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-3\right)^2}=\left(\dfrac{1+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}\right).\dfrac{\left(\sqrt{x}-3\right)^2}{\sqrt{x}+1}=\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
b)Với x>0,x\(\ne\)9
\(Q< 0< =>\dfrac{\sqrt{x}-3}{\sqrt{x}}< 0\)
\(< =>\sqrt{x}-3< 0\left(Vì\sqrt{x}>0\right)\)
\(< =>\sqrt{x}< 3\)
\(< =>x< 9\)
Kết hợp với ĐKXĐ ta được
0<x<9