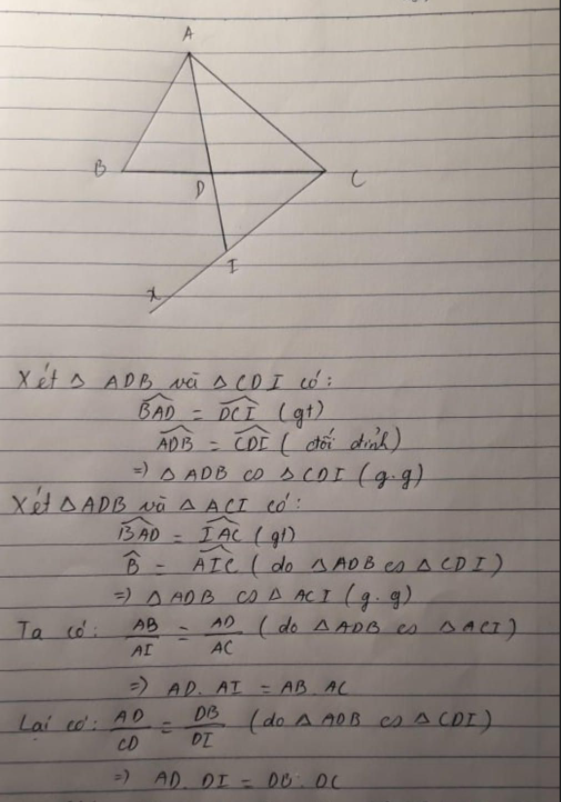Cho tam giác ABC (AB\(\ne\)AC) , phân giác AD. Ở miền ngoài tam giác , vẽ Cx sao cho BCx = BDA. gọi I giao điểm Cx và AD. c/m AD.AD=AB.AC - BD.DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 4 2021
a) Xét ΔADB và ΔCDI có
\(\widehat{ADB}=\widehat{CDI}\)(hai góc đối đỉnh)
\(\widehat{BAD}=\widehat{ICD}\)(gt)
Do đó: ΔADB\(\sim\)ΔCDI(g-g)
27 tháng 7 2018
a, Xét tam giác ADB và tam giác CDI có:
góc ADB = góc CDI (đối đỉnh)
góc BAD = góc DCI (gt)
Do đó: Tam giác ADB đồng dạng với tam giác CDI (g.g) (1)
Suy ra: góc ABD = góc DIC
b, Tam giác ADB đồng dạng với tam giác ACI (g.g) (2)
Suy ra: AD/AC = AB/AI
c, Từ (1),ta thấy: AD/CD = DB/DI nên AD.DI = BD.BC
Từ (2),ta có: AD/AC = AB/AI nên AD.AI = AB.AC
Do đó: AD(AI-DI) = AB.AC - BD.BC
AD^2 = AB.AC -BD.BC
Bài bạn đưa ra hơi khó đấy.Chúc bạn học tốt.
27 tháng 6 2023
a: Xét ΔDAB và ΔDCI có
góc DAB=góc DCI
góc ADB=góc CDI
=>ΔDAB đồng dạng với ΔDCI
=>DA/DC=DB/DI
=>DA/DB=DC/DI
Xét ΔDAC và ΔDBI có
DA/DB=DC/DI
góc ADC=góc BDI
=>ΔDAC đồng dạng với ΔDBI
b: Xét ΔABD và ΔAIC có
góc ABD=góc AIC
góc bAD=góc IAC
=>ΔABD đồng dạng với ΔAIC
=>AB/AI=AD/AC
=>AB*AC=AD*AI
