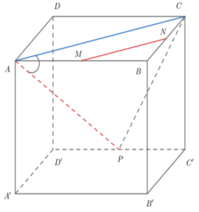
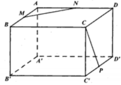
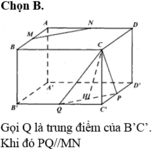
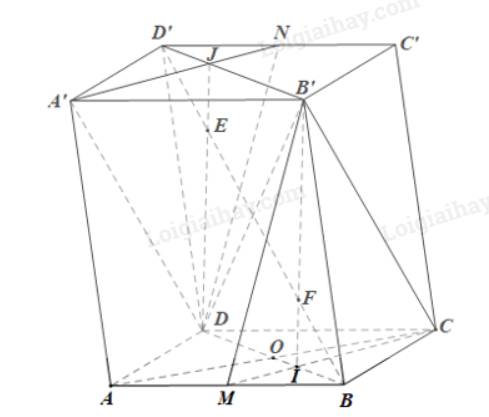
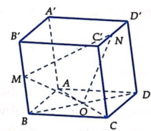
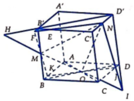
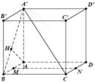
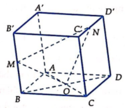
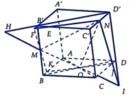
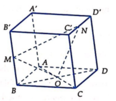
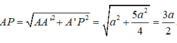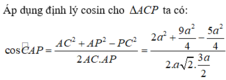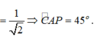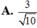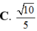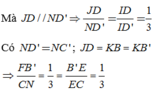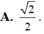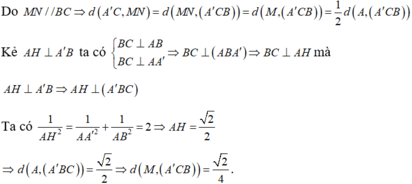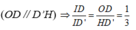Cho hình hộp ABCD.A’B’C’D’. Xét các điểm M và N lần lượt thuộc các đường thẳng A’C và C’D sao cho vecto MA'= -3 vecto MC , vecto NC'= - vecto ND . Đặt vectoBA = A, vecto BB' =b , vecto BC= c. . Hãy biểu thị các vectơ BM và BN qua các vectơ a,b,c? CM: MN// BD'