bài 2 toán 5 trang 108'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SN
15 tháng 10 2021
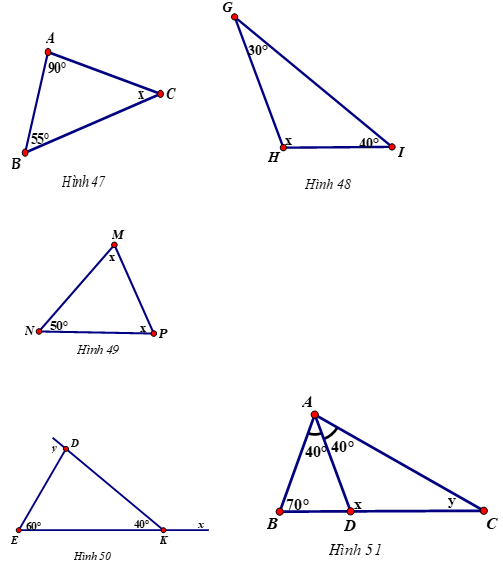
Áp dụng định lý tổng ba góc trong một tam giác bằng 180º ta có:
- Hình 47
x + 90o + 55o = 180o
x = 180o - 90o - 55o
x = 35o
- Hình 48
x + 30o + 40o = 180o
x = 180o - 30o - 40o
x = 110o
- Hình 49
x + x + 50o = 180o
2x = 180o - 50o
x = 65o
Áp dụng định lý góc ngoài của tam giác ta có:
- Hình 50
y = 60o + 40o
y = 100o
x + 40o = 180o (2 góc kề bù)
x = 140o
- Hình 51
Áp dụng định lý góc ngoài trong tam giác ABD có: x = 70º + 40º = 110º
Áp dụng định lý tổng ba góc trong tam giác ADC có:
y + 110º + 40º = 180º ⇒ y = 30º.
LT
11
8 tháng 2 2022
TK :
Lời giải chi tiết
a) Các cạnh bằng nhau của hình hộp chữ nhật là:
AB = CD = MN = PQ
AD = BC = MQ = NP
AM = BN = CP = DQ
b) Diện tích mặt đáy MNPQ là:
6 × 3 = 18 (cm2)
Diện tích của mặt bên ABNM là:
6 × 4 = 24 (cm2)
Diện tích của mặt bên BCPN là:
4 × 3 = 12 (cm2)
Đáp số: b) Mặt đáy MNPQ: 18cm2;
Mặt bên ABNM: 24cm2;
Mặt bên BCPN: 12cm2.
NX
0
ND
0
23 tháng 12 2016
giải hơi sơ sài ko đầy đủ nếu làm ko đầy đủ lớp trưởng kiểm tra thì chết
NN
9
14 tháng 10 2021
TL
a) Ta có ˆBIKBIK^ là góc ngoài tại đỉnh II của ΔBAIΔBAI.
Nên ˆBIK=ˆBAI+ˆABI>ˆBAIBIK^=BAI^+ABI^>BAI^
Mà ˆBAK=ˆBAIBAK^=BAI^
Vậy ˆBIK>ˆBAKBIK^>BAK^ (1)
b) Ta có ˆCIKCIK^ là góc ngoài tại đỉnh II của ΔAICΔAIC
nên ˆCIK=ˆCAI+ˆICA>ˆCAICIK^=CAI^+ICA^>CAI^
Hay ˆCIK>ˆCAICIK^>CAI^ (2)
Từ (1) và (2) ta có:
ˆBIK+ˆCIK>ˆBAK+ˆCAIBIK^+CIK^>BAK^+CAI^
⇒ˆBIC>ˆBAC⇒BIC^>BAC^.
Hok tốt nha bn
#Kirito
QC
1
TL
a) Các cạnh bằng nhau của hình hộp chữ nhật là:
AB = CD = MN = PQ
AD = BC = MQ = NP
AM = BN = CP = DQ
b) Diện tích mặt đáy MNPQ là:
6 × 3 = 18 (cm2)
Diện tích của mặt bên ABNM là:
6 × 4 = 24 (cm2)
Diện tích của mặt bên BCPN là:
4 × 3 = 12 (cm2)
Đáp số: b) Mặt đáy MNPQ: 18cm2;
Mặt bên ABNM: 24cm2;
Mặt bên BCPN: 12cm2.