cho ΔABC nhọn, các đg cao BD và CE cắt nhau tại H. Đg vuông góc với AB tại B, đg vuông góc với AC tại C cắt nhau tại K, MB=MCa) ΔADB \(\sim\)ΔAEC và ΔAED \(\sim\)ΔACBb)HE.HC=HD.HBc) H, M, K thẳng hàng và ∠AED=∠ACBd) AH cắt BC tại O. C/m: BE.AB+CD.AC=\(^{BC^2}\)e)...
Đọc tiếp
cho ΔABC nhọn, các đg cao BD và CE cắt nhau tại H. Đg vuông góc với AB tại B, đg vuông góc với AC tại C cắt nhau tại K, MB=MC
a) ΔADB \(\sim\)ΔAEC và ΔAED \(\sim\)ΔACB
b)HE.HC=HD.HB
c) H, M, K thẳng hàng và ∠AED=∠ACB
d) AH cắt BC tại O. C/m: BE.AB+CD.AC=\(^{BC^2}\)
e) c/m: \(\dfrac{HO}{AO}+\dfrac{HD}{BD}+\dfrac{HE}{CE}=1\)
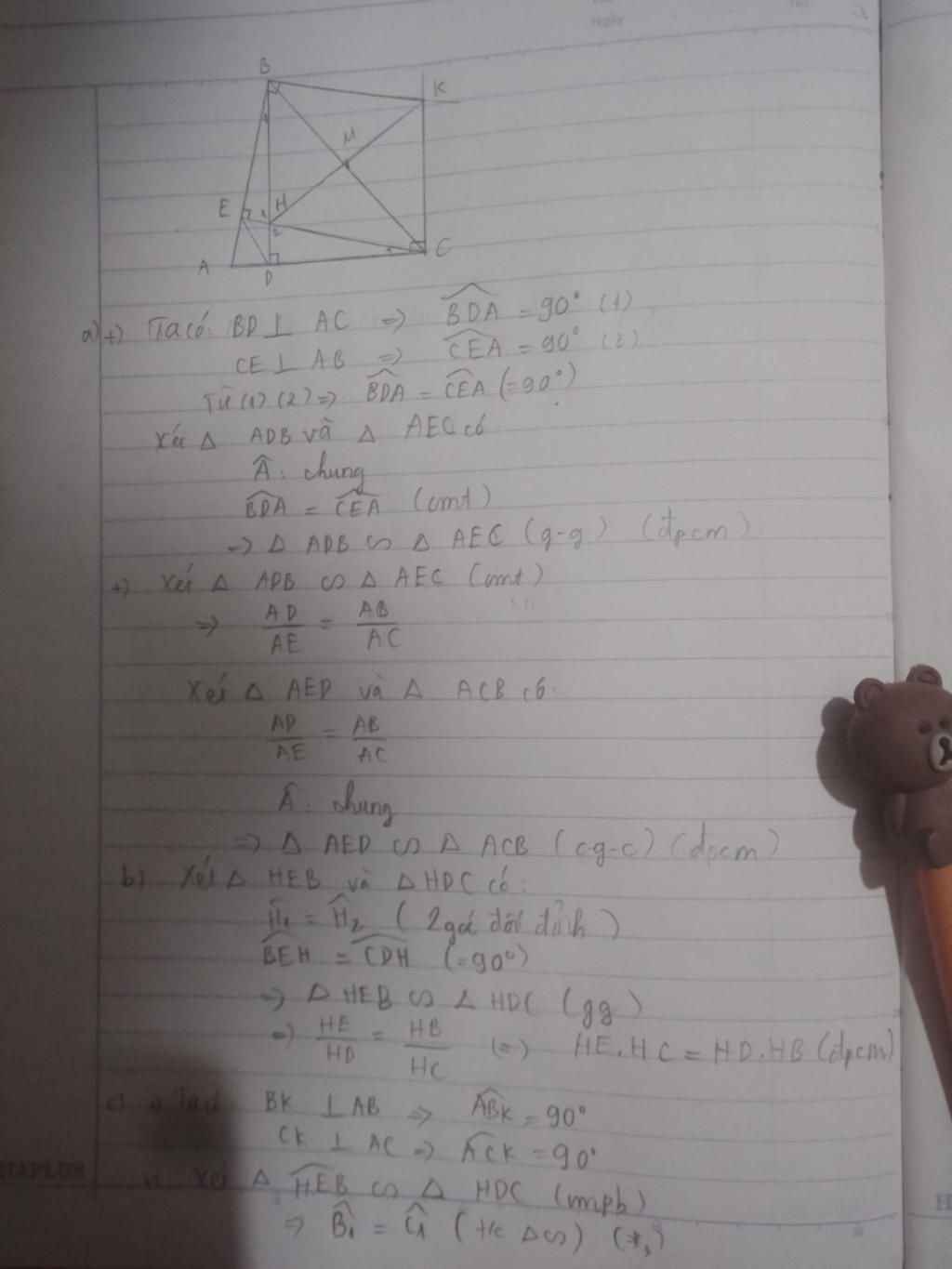
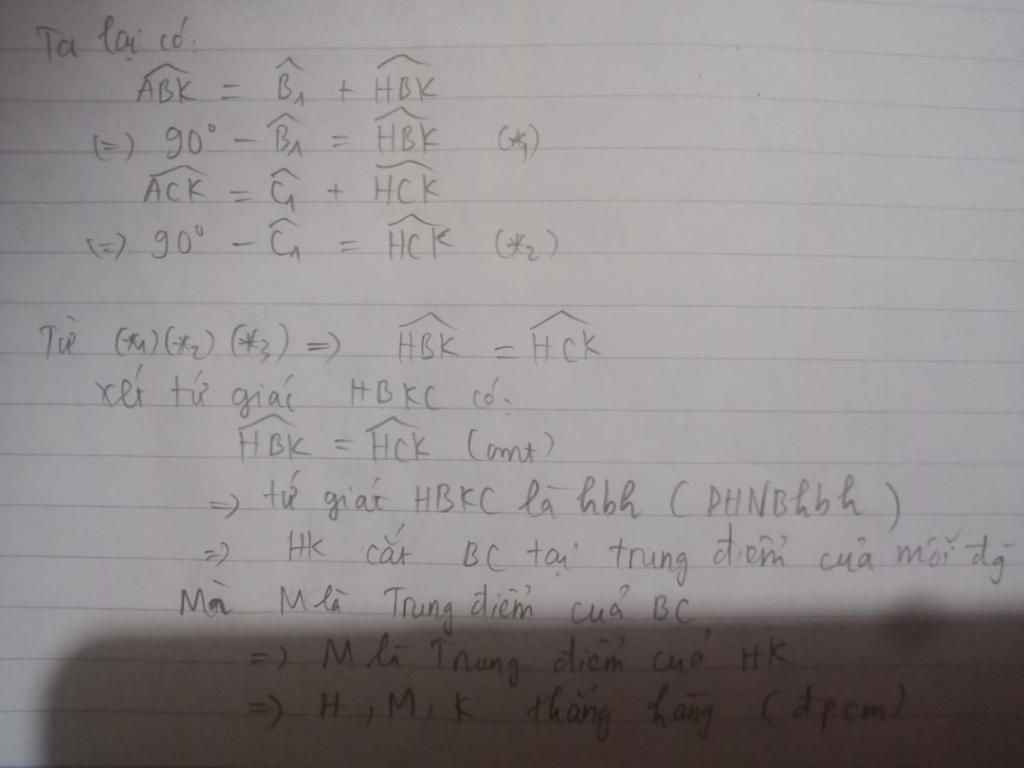
∠ nghĩa là j thế , xl hơi ngu:<
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
DO đó: ΔADB∼ΔAEC
Suy ra: AD/AE=AB/AC
hay AD/AB=AE/AC
Xét ΔADE và ΔABC có
AD/AB=AE/AC
\(\widehat{DAE}\) chung
Do đó: ΔADE∼ΔABC
b: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔHEB\(\sim\)ΔHDC
Suy ra: HE/HD=HB/HC
hay \(HE\cdot HC=HB\cdot HD\)