Chứng minh rằng với mọi b > 0, ta có:
a) \(\frac{a}{b}>1\Leftrightarrow a>b\) b) \(\frac{a}{b}\)\(<1\)\(\Leftrightarrow\)\(a\)\(<\)\(b\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a+b+c+2=abc\)
\(\Leftrightarrow\left(a+1\right)\left(b+1\right)+\left(b+1\right)\left(c+1\right)+\left(c+1\right)\left(a+1\right)=\left(a+1\right)\left(b+1\right)\left(c+1\right)\)
\(\Leftrightarrow\frac{1}{a+1}+\frac{1}{b+1}+\frac{1}{c+1}=1\)

a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
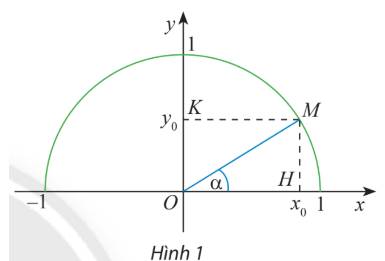
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)

a) \(\frac{x}{3}-\frac{1}{y}=\frac{1}{6}\)
Quy đồng \(\frac{x}{3}\)với \(\frac{1}{6}\). Ta có:
\(\frac{x}{3}=\frac{x.6}{3.6}=\frac{x6}{18}\)
\(\frac{1}{6}=\frac{1.3}{6.3}=\frac{3}{18}\)
\(\Rightarrow\frac{x}{3}-\frac{1}{y}=\frac{1}{6}\Leftrightarrow\frac{x6}{18}-\frac{1}{y}=\frac{3}{18}\)
Quy đồng \(\frac{1}{y}\)với \(\frac{3}{18}\). Ta có:
Đặt mẫu số chung: 18. Ta có:
\(\frac{1}{y}=\frac{18}{18}\) ( Vì khi quy đồng mẫu số của (1/y) phải là 18. Nên (1/y) = (1.18)/18 = (18/18) )
Vì y là mẫu. Suy ra y = 18
\(\Rightarrow\frac{x6}{18}-\frac{1}{y}=\frac{3}{18}\Leftrightarrow\frac{x6}{18}-\frac{18}{18}=\frac{3}{18}\)
\(\Leftrightarrow\frac{x6}{18}=\frac{18}{18}+\frac{3}{18}\Leftrightarrow\frac{x6}{18}=\frac{21}{18}\)
\(\Rightarrow x6=21\Rightarrow x=\frac{21}{6}=\frac{7}{2}\) ( và vì x là tử suy ra x = 7)
Vậy .....
b) Ta có: \(\left(3a+11b\right)⋮17\Leftrightarrow\left(5a+17b\right)⋮17\)
\(\Rightarrow\left(a+b\right)⋮17\)
Vì ( a + b) chia hết cho 17
\(\Rightarrow\left(..a+..b\right)⋮17\). Thế số vào chỗ ". . " Ta có:
\(\left(..a+..b\right)=\left(5a+17b\right)⋮17\left(ĐPCM\right)\)

`a) 2 ( a^2 + b^2 ) >= ( a + b )^2`
`<=> 2a^2 + 2b^2 >= a^2 + 2ab + b^2`
`<=> a^2 - 2ab + b^2 >= 0`
`<=> ( a - b )^2 >= 0` (Luôn đúng `AA a,b`)
`=>` Đẳng thức được c/m
_________________________________________
`b) a^2 + b^2 + c^2 >= ab + bc + ca`
`<=> 2a^2 + 2b^2 + 2c^2 >= 2ab + 2bc + 2ca`
`<=> ( a^2 - 2ab + b^2 ) + ( b^2 - 2bc + c^2 ) + ( c^2 - 2ca + a^2 ) >= 0`
`<=> ( a - b )^2 + ( b - c )^2 + ( c - a )^2 >= 0` (Luôn đúng `AA a,b,c`)
`=>` Đẳng thức được c/m

\(a^2+b^2+4\ge ab+2\left(a+b\right)\)
\(\Leftrightarrow2a^2+2b^2+8\ge2ab+4\left(a+b\right)\)
\(\Leftrightarrow2a^2+2b^2+8-2ab-4a-4b\ge0\)
\(\Leftrightarrow a^2-2ab+b^2+a^2-4a+4+b^2-4b+4\ge0\)
\(\Leftrightarrow\left(a-b\right)^2+\left(a-2\right)^2+\left(b-2\right)^2\ge0\) (Luôn đúng)
Vậy đẳng thức ban đầu được chứng minh.
Điều đơn giản bạn tự suy luận sẽ ra thôi đâu cần cm làm gì
xong hết rồi chứng minh gì nữa nếu a>b <=>a/b > 1 vd a = 3, b = 2 a/b =3/2 =1.5 > 1
Ngược lại ....................