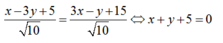trình bày cách giải bài này giúp mình với
Trong mặt phẳng Oxy, phương trình đường phân giác góc nhọn của góc tạo bởi 2 đường thẳng
d1: 3x+4y-3=0
d2: 4x+3y-1=0 là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
Gọi \(\overrightarrow{n}=\left(a;b\right)\) là 1 vtpt của đường thẳng d' cần tìm
Do d' tạo với d 1 góc bằng 45 độ
\(\Rightarrow cos\left(d;d'\right)=\dfrac{\left|2a+3b\right|}{\sqrt{2^2+3^2}.\sqrt{a^2+b^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}\left|2a+3b\right|=\sqrt{13\left(a^2+b^2\right)}\)
\(\Leftrightarrow2\left(2a+3b\right)^2=13\left(a^2+b^2\right)\)
\(\Leftrightarrow5a^2-5b^2-24ab=0\)
\(\Rightarrow\left[{}\begin{matrix}a=5b\\b=-5a\end{matrix}\right.\) \(\Rightarrow\) chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(5;1\right)\\\left(a;b\right)=\left(1;-5\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}5\left(x-3\right)+1\left(y-6\right)=0\\1\left(x-3\right)-5\left(y-6\right)=0\end{matrix}\right.\) \(\Leftrightarrow...\)
CM
21 tháng 8 2018
Cho 2 đường thẳng cắt nhau d 1 : a 1 x + b 1 y + c 1 = 0 v à d 2 : a 2 x + b 2 y + c 2 = 0 .
Khi đó, phương trình đường phân giác tạo bởi 2 đường thẳng là:
a 1 x + b 1 y + c 1 a 1 2 + b 1 2 = ± a 2 x + b 2 y + c 2 a 2 2 + b 2 2
Áp dụng công thức ta có phương trình hai phân giác là:
3 x − 4 y + 1 3 2 + ( − 4 ) 2 = ± x + 3 1 2 + 0 2 ⇔ 3 x − 4 y + 1 5 = ± ( x + 3 ) ⇔ 3 x − 4 y + 1 = ± 5 x + 3 ⇔ 2 x + 4 y + 14 = 0 8 x − 4 y + 16 = 0 ⇔ x + 2 y + 7 = 0 2 x − y + 4 = 0
ĐÁP ÁN C
CM
20 tháng 5 2017
Gọi M(x;y) là điểm thuộc đường phân giác của góc tạo bởi hai đường thẳng đã cho
+) Ta có:
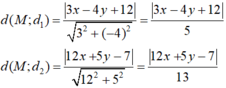
+) Do điểm M thuộc đường phân giác của góc tạo bởi hai đường thẳng d1 và d2 nên điểm M cách đều hai đường thẳng trên: d( M; d1)= d(M, d2 )
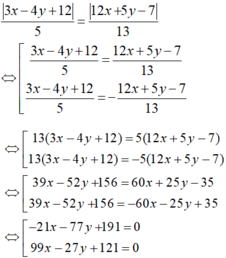
Vậy phương trình 2 đường phân giác của góc tạo bởi hai đường thẳng đã cho là:
-21 x – 77y + 191= 0 và 99x – 27y + 121 =0
10 tháng 3 2022
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
CM
6 tháng 11 2018
Đáp án B
Ta có: 
là véc tơ pháp tuyến của d; d’ và 
Nên phương tình đường phân giác của góc nhọn là:
