Cho điểm M nằm trong tam giác ABC. Chứng minh rằng: MA + MC < AB + BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kéo dài AM cắt BC tại D \(\Rightarrow\) D nằm giữa B và C
Áp dụng BĐT tam giác ABD:
\(AB+BD>AD\Rightarrow AB+BD>AM+MD\)
Áp dụng BĐT tam giác MCD:
\(MD>MC-CD\)
\(\Rightarrow AB+BD+MD>AM+MD+MC-CD\)
\(\Rightarrow AB+BD+CD>AM+MC\)
\(\Rightarrow AB+BC>AM+MC\)

$M$ là điểm nằm trong $ΔABC$
nên ta có các tam giác $ΔMAB;MAC;MBC$
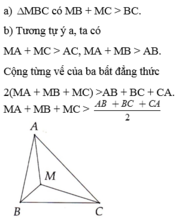
Xét $ΔMAB$ có: $MA+MB>AB$ (quan hệ giữa 3 cạnh trong 1 tam giác;bất đẳng thức tam giác)
tương tự $ΔMAC$ có: $MA+MC>AC$
$ΔMBC$ có: $MB+MC>BC$
nên $MA+MB+MA+MC+MB+MC>AB+BC+CA$
suy ra $2.(MA+MB+MC)>AB+BC+CA$
hay $MA+MB+MC>\dfrac{AB+BC+CA}{2}$


Không làm mà đòi có ăn thì ............................................
Nguôi ta de len day de giúp chu ko de cho may Súa nhe con .......
hình bạn tự vẽ nhé
ta có do điểm M nằm trong tam giác ABC nên \(\widehat{AMB}\) + \(\widehat{AMC}\) + \(\widehat{CMB}\) \(=360^0\)
\(\Rightarrow\) trong 3 góc này nhiều nhất chỉ có 1 góc bằng \(90^0\) và 2 góc còn lại phải lớn hơn \(90^0\) bởi nếu có 2 góc = \(90^0\)
thì khi đó M sẽ là chân đường vuông góc kẻ từ một đỉnh,M sữ ko nằm trong tam giác
xét tam giác AMB có AMB sẽ lớn hơn hoặc bằng \(90^0\) nên AB là cạnh lớn nhất tong tam giác đó(quan hệ cạnh đối diện vs góc)
\(\Rightarrow\) AB > MA
tượng tự,CM BC > MC
\(\Rightarrow\) AB+BC > MA + MC (ĐPCM)
TL
ta có do điểm M nằm trong tam giác ABC nên \(\widehat{AMB}\) + \(\widehat{AMC}\) + \(\widehat{CMB}\) \(=360^0\)
\(\Rightarrow\) trong 3 góc này nhiều nhất chỉ có 1 góc bằng \(90^0\) và 2 góc còn lại phải lớn hơn \(90^0\) bởi nếu có 2 góc = \(90^0\)
thì khi đó M sẽ là chân đường vuông góc kẻ từ một đỉnh,M sữ ko nằm trong tam giác
xét tam giác AMB có AMB sẽ lớn hơn hoặc bằng \(90^0\) nên AB là cạnh lớn nhất tong tam giác đó(quan hệ cạnh đối diện vs góc)
\(\Rightarrow\) AB > MA
tượng tự,CM BC > MC
\(\Rightarrow\) AB+BC > MA + MC (ĐPCM)