giúp em với ạ!
Cho tam giác ABC và trọng tâm G của nó. Chứng minh rằng tam giác ABC là tam giác cân khi và chỉ khi AB + GB = AC + GC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì G là trọng tâm của tam giác ABC ta có :
AG=2/3 AN
BG=2/3 BQ (1)
CG=2/3 CM (2)
mà 2 tam giác ACM=ABQ ( g-c-g)
suy ra CM=BQ (cạnh tương ứng) (3)
từ (2) và (3) suy ra BG=CG
>>>>>>.........''tớ chỉ pk lmf tới đây thui''.........<<<<<<<<<<

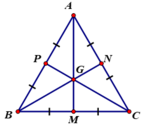
a) tg ABC đều
mà G là trọng tâm
=> AG,CG,BG là dg pg
thì có các tg AGB, AGC,BGC cân
=> AG=CG=BG
b) tg APN cân tại A(tự cm)
mà góc A(lớn ) = 60độ
=> tg APN đều => góc ANP=góc ACB
=>PN//BC(...)
CMT vs các tg MNC,PMB
c)tg MNC=tgPMB=tg PNA(M,N,P lần lượt là tđ của BC,AC,AB)
=> MN=PM=PN
=> tg PMN đều

Từ giả thiết suy ra với mọi O đều có ?
\(\overrightarrow{OG}=\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)\) và \(\overrightarrow{OG_1}=\frac{1}{3}\left(\overrightarrow{OA}_1+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\)
Mà :
\(\overrightarrow{OG_2=}\frac{1}{3}.\left(\overrightarrow{OGa}+\overrightarrow{OG_b}+\overrightarrow{OG_c}\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB_1}+\overrightarrow{OC_1}\right)+\frac{1}{3}\left(\overrightarrow{OB}+\overrightarrow{OC_1}+\overrightarrow{OA_1}\right)+\frac{1}{3}\left(\overrightarrow{OC}+\overrightarrow{OA_1}+\overrightarrow{OB_1}\right)\right)\)
\(=\frac{1}{3}\left(\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)+\frac{2}{3}\left(\overrightarrow{OA_1}+\overrightarrow{OB_1}+\overrightarrow{OC}_1\right)\right)\)
\(=\frac{1}{3}\overrightarrow{OG}+\frac{2}{3}\overrightarrow{OG_1}\)
Suy ra :
\(3\overrightarrow{OG_2}=\overrightarrow{OG}+2\overrightarrow{OG_1}\) với mọi O. Điều này có nghĩa là \(G,G_1,G_2\) thẳng hàng => Điều phải chứng minh

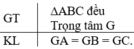
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
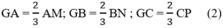
Từ (1) , (2) ⇒ GA = GB = GC.