Giúp mình với tìm số nguyên n để A=6n+7 phần 2n+3 nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) A = \(\dfrac{6n+7}{2n+3}\) = \(\dfrac{6n+9}{2n+3}\) − \(\dfrac{2}{2n+3}\) nguyên
⇔ 2n + 3 ∈ Ư(2) = {-2; -1; 1; 2}
⇔ 2n ∈ {-5; -4; -2; -1}
Vì n nguyên nên n ∈ {-2; -1}

a)(6n-4) chia hết cho (1-2n)
Ta có (1-2n)=3(1-2n)=3-6n
\(\Rightarrow\)(6n-4+3-6n)\(⋮\)(1-2n)
\(\Rightarrow\)(-1)\(⋮\)(1-2n)\(\Rightarrow\)(1-2n)\(\in\) Ư(1)={±1}
Ta có bảng
| 1-2n | -1 | 1 |
| 2n | 2 | 0 |
| n | 1 | 0 |
Vậy...
T.i.c.k cho mình nhé
- #TM

a) \(A=\frac{6n+7}{2n+3}=\frac{6n+9}{2n+3}-\frac{2}{2n+3}\) nguyên
<=> 2n + 3 thuộc Ư(2) = {-2; -1; 1; 2}
<=> 2n thuộc {-5; -4; -2; -1}
Vì n nguyên nên n thuộc {-2; -1}
b) A có GTNN <=> \(\frac{2}{2n+3}\) có GTLN
<=> 2n + 3 là số nguyên dương nhỏ nhất
<=> 2n + 3 = 1
<=> 2n = -2
<=> n = -1
a)\(A=\frac{6n+7}{2n+3}=\frac{2n+2n+2n+3+4}{2n+3}=\frac{4}{2n+3}\)
\(\Rightarrow2n+3\in\text{Ư}\left(4\right)=\left\{1;2;4;-1;-2;-4\right\}\)
Nếu 2n+3 = 1 => n = -2 (nhận)
Nếu 2n+3 = 2 => n =-0,5 (loại)
Nếu 2n + 3 = 4 => n = 3,5 (loại)
Nếu 2n + 3 = -1 => n = 1 (nhận)
Nếu 2n + 3 = -2 => n = -2,5 (loại)
Nếu 2n + 3 = -4 => n =-3,5 (loại)
Vậy n \(\in\) {-2;1}
b) A GTNN => \(\frac{2}{2n+3}\) có GTLN
=> 2n + 3 là số nguyên dương nhỏ nhất
=> 2n + 3 = 1
=> 2n = -2
=> n = -1

\(A=\frac{1-6n}{2n-3}=\frac{-6n+9-8}{2n-3}=-3+\frac{-8}{2n-3}\)
Để \(A\in Z\Rightarrow\frac{-8}{2n-3}\in Z\)
\(\Rightarrow-8⋮2n+3\)
\(\Rightarrow2n+3\inƯ\left(-8\right)\)
\(\Rightarrow2n+3\in\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
Vì \(2n+3\)là số lẻ
\(\Rightarrow2n+3\in\left\{1;-1\right\}\)
\(\Rightarrow2n\in\left\{-2;-4\right\}\)
\(\Rightarrow n\in\left\{-1;-2\right\}\)
Vậy...
A=\(\frac{1-6n}{2n-3}\)
=\(\frac{-6n+9-8}{2n-3}\)
= \(-3+\frac{-8}{2n-3}\)
để \(A\inℤ\Leftrightarrow\frac{-8}{2n-3}\inℤ\)
\(\Leftrightarrow-8⋮2n+3\)
\(\Leftrightarrow2n+3\inƯ\left(-8\right)\)
MÀ Ư(-8)=\(\hept{\pm1;\pm2;\pm4;\pm8}\)
VÌ 2n+3 là số lẻ nên ta có bảng:
| 2n+3 | 1 | -1 |
| 2n | -2 | -4 |
| n | -1 | -2 |
vậy n\(\in\hept{-1;-2}\)
thì A là 1 số nguyên

Ta có:
\(\dfrac{2n-1}{2n+3}=\dfrac{2n+3-4}{2n+3}\)\(=1-\dfrac{4}{2n+3}\)
Để \(\dfrac{2n-1}{2n+3}\) là số nguyên thì \(2n+3\inƯ\left(4\right)\)
Ta có bảng:
| \(2n+3\) | \(-4\) | \(-2\) | \(-1\) | \(1\) | \(2\) | \(4\) |
| \(2n\) | \(-7\) | \(-5\) | \(-4\) | \(-2\) | \(-1\) | \(1\) |
| \(n\) | \(-\dfrac{7}{2}\left(loại\right)\) | \(-\dfrac{5}{2}\left(loại\right)\) | \(-2\) | \(-1\) | \(-\dfrac{1}{2}\left(loại\right)\) | \(\dfrac{1}{2}\left(loại\right)\) |
Vậy \(n\in\left\{-2;-1\right\}\)
Để A nguyên thì 2n-1 chia hết cho 2n+3
=>2n+3-4 chia hết cho 2n+3
=>\(2n+3\in\left\{1;-1;2;-2;4;-4\right\}\)
mà n nguyên
nên \(n\in\left\{-1;-2\right\}\)
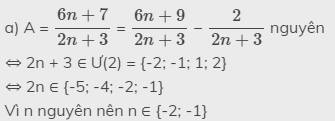
\(\frac{6n+7}{2n+3}=\frac{6n+9-2}{2n+3}=\frac{3\left(2n+3\right)-2}{2n+3}=3-\frac{2}{2n+3}\)
Đê phân số số trên là số nguyên thì 2n+3 phải là ước của 2
\(\Rightarrow2n+3=\left\{-2;-1;1;2\right\}\Rightarrow n=\left\{-\frac{5}{2};-2;-1;-\frac{1}{2}\right\}\)
Do n nguyên nên n={-2;-1}