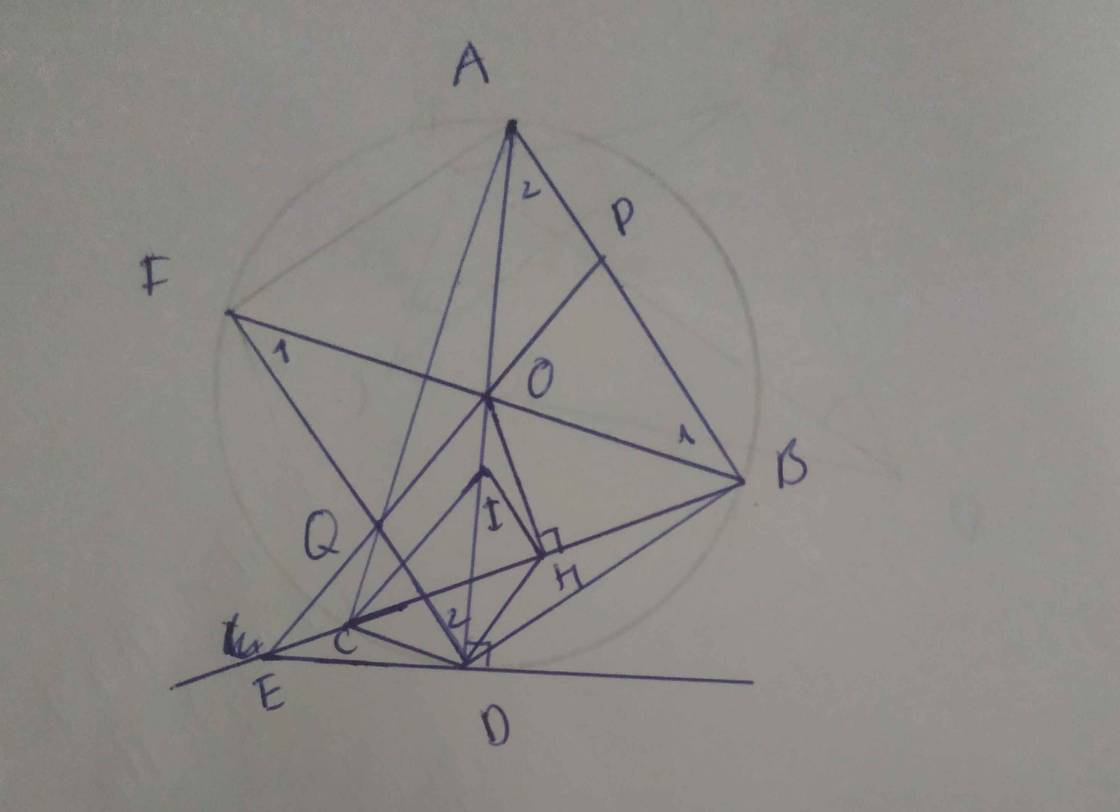
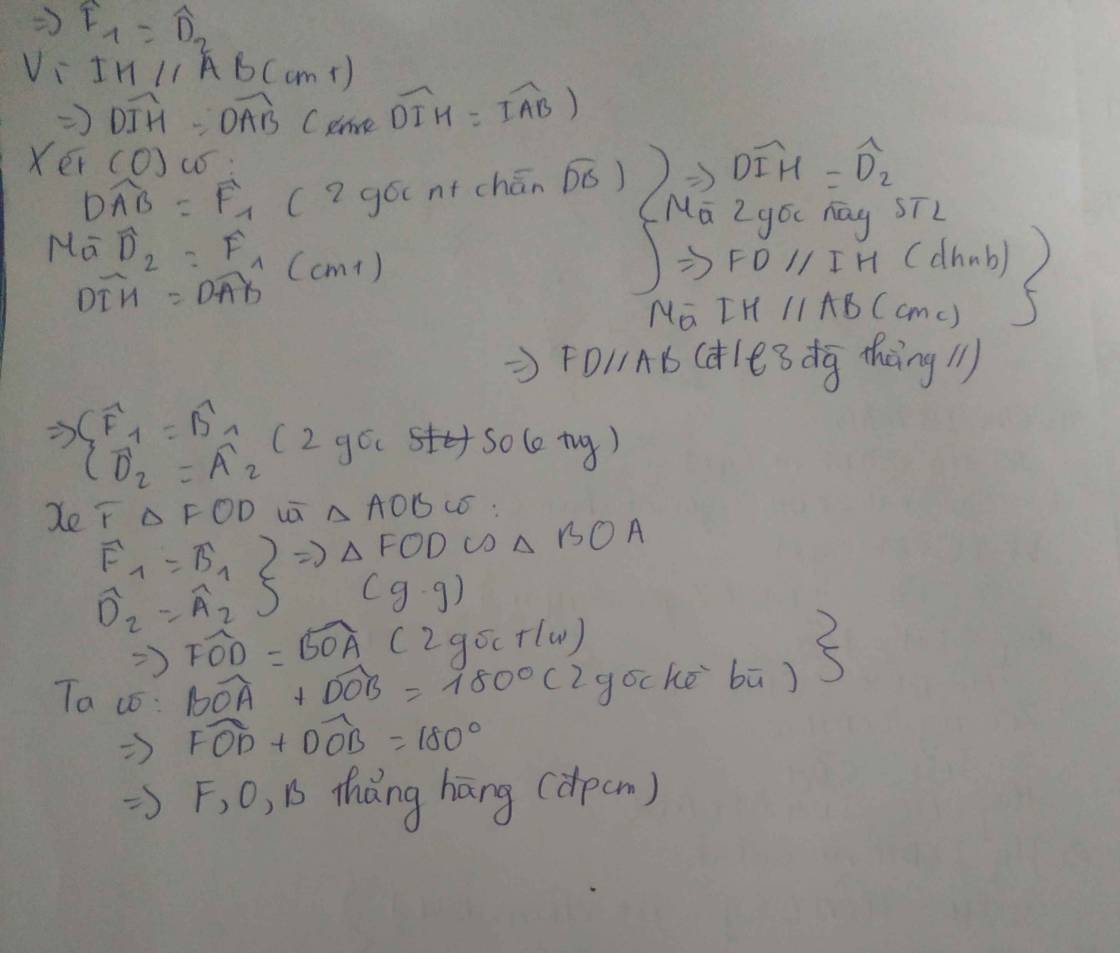Cho ABC có AC AB , nôi tiếp đường tròn O R ; , Gọi AD và AE theo thứ tự
là phân giác trong, phân giác ngoài của ABC ( D và E thuộc BC ), biết AD AE , AD cắt O R ; tại
điểm thứ hai là F .
a) Chứng minh FCB cân.
b) Tính sđ AC sđ BF .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2023
a: góc BDC=góc BEC=90 độ
=>CD vuông góc AB, BE vuông góc AC
góc ADH+góc AEH=180 độ
=>ADHE nội tiếp
5 tháng 7 2023
a: ΔABC vuông tại A nên O là trung điểm của BC
Xét ΔCAB có CF/CA=CO/CB
nên FO//AB
=>FO vuông góc AC
góc AHO+góc AFO=180 độ
=>AHOF nội tiếp đường tròn đường kính AO
=>I là trung điểm của AO
b: (O) và (I) đều đi qua A
OI=OA-IA=R-r'
=>(O) tiếp xúc (I) tại A
31 tháng 7 2023
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
13 tháng 1 2022
a: Xét (O) có
ΔABC nội tiếp
AB là đường kính
Do đó: ΔABC vuông tại C
b: Xét ΔABC vuông tại C có CH là đường cao
nên \(AH\cdot AB=AC^2\left(1\right)\)
Xét ΔMAB vuông tại A có AC là đường cao
nên \(MC\cdot BC=AC^2\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot AB=MC\cdot BC\)