Với giá trị nào của x thì mỗi căn thức sau xác định:
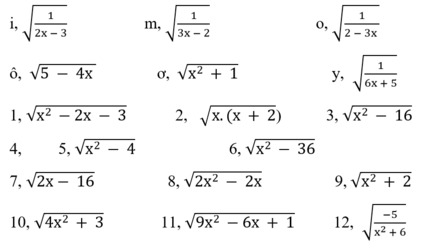
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phân thức 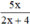 xác định
xác định
⇔ 2x + 4 ≠ 0
⇔ 2x ≠ -4
⇔ x ≠ -2
Vậy với mọi x ≠ -2 thì phân thức 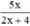 xác định.
xác định.

Phân thức 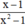 xác định
xác định
⇔ x2 – 1 ≠ 0
⇔ (x – 1)(x + 1) ≠ 0
⇔ x – 1 ≠ 0 và x + 1 ≠ 0
⇔ x ≠ 1 và x ≠ -1.
Vậy với mọi x ≠ ±1 thì phân thức 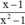 xác định
xác định

\(\sqrt{\dfrac{1}{-1+x}}=\sqrt{\dfrac{1}{x-1}}\) có nghĩa khi:
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}\ge0\\x-1\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x\ne1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\x\ne1\end{matrix}\right.\)
\(\Leftrightarrow x>1\)
\(ĐKXĐ:\dfrac{1}{-1+1x}>0\Leftrightarrow-1+1x< 0\\ \Leftrightarrow x< -1\)

\(\left[{}\begin{matrix}x\ge1\\x\le-1\end{matrix}\right.\)

\(\sqrt{-\left|x+5\right|}\)có nghĩa khi và chỉ khi \(-\left|x+5\right|\ge0\Leftrightarrow\left|x+5\right|\le0\)
Mà\(\left|x+5\right|\)là không âm nên đề bài thỏa mãn khi và chỉ khi \(\left|x+5\right|=0\Leftrightarrow x=-5\)

`Answer:`
a) Phân tích \(\frac{7x}{15x-5}\) được xác định khi: \(15x-5\ne0\Rightarrow15x\ne5\Rightarrow x\ne\frac{1}{3}\)
b) \(\frac{x+4}{x^2-9}=\frac{x+4}{\left(x-3\right)\left(x+3\right)}\)
Vậy điều kiện xác định: `x\ne+-3`
c) Vì phân thức có chứa ẩn dưới mẫu nên để cho phân thức xác định thì:
\(36x^2-25\ne0\Rightarrow36x^2\ne25\Rightarrow x^2\ne\frac{25}{36}\Rightarrow x\ne\pm\frac{5}{6}\)
d) Phân thức xác định khi \(x^2+2x+3\ne0\Rightarrow\left(x+1\right)^2+2\ne0\)
Nhận thấy \(\left(x+1\right)^2+2\ge2>0\forall x\)
\(\Rightarrow\left(x+1\right)^2+2\ne0\) (Luôn đúng)
Vậy phân thức trên được xác định với mọi `x`

c) Ta có: \(\sqrt{x^2-3}\)
Có nghĩa khi: \(x^2-3\ge0\)
\(\Leftrightarrow x^2\ge3\)
\(\Leftrightarrow x\ge\sqrt{3}\)
e) Ta có: \(\sqrt{x\left(x+2\right)}\)
Có nghĩa khi: \(x\left(x+2\right)\ge0\)
\(\Leftrightarrow x\ge-2\)
Sai rồi nha
\(x\left(x+2\right)\ge0\) thì
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x\le0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge0\\x\ge-2\end{matrix}\right.\\\left\{{}\begin{matrix}x\le0\\x\le-2\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x\le-2\end{matrix}\right.\)
(ngoặc vuông là hoặc , ngoặc nhọn là và)
| 🌸 \(mathew\) |
\(i.x>\dfrac{3}{2}\)
\(m.x>\dfrac{2}{3}\)
\(o.x< \dfrac{2}{3}\)
\(ô.x\le\dfrac{5}{4}\)
\(ơ.mọi.x\in Z\)
\(y.x>\dfrac{-5}{6}\)