 Giúp mình bài 4 với ạ cảm ơnnn :333
Giúp mình bài 4 với ạ cảm ơnnn :333
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 6.
a)Công suất ấm: \(P=\dfrac{A}{t}=\dfrac{900\cdot1000}{10\cdot60}=1500W\)
Dòng điện qua ấm: \(I=\dfrac{P}{U}=\dfrac{1500}{220}=\dfrac{75}{11}A\)
Điện trở dây nung: \(R=\dfrac{U}{I}=\dfrac{220}{\dfrac{75}{11}}=\dfrac{484}{15}\Omega\)
b)Điện năng tiêu thụ trong 1 tháng (30 ngày):
\(T=900\cdot1000\cdot30\cdot3600=9,72\cdot10^{10}J=27000kWh\)
Tiền điện phải trả: \(T=27000\cdot1500=40500\left(k.đồng\right)\)
c)Công suất tiêu thụ thực:
\(P=UI=\dfrac{U^2}{R}=\dfrac{110^2}{\dfrac{484}{15}}=375W\)
Bài 7.
CTM: \(\left(Đ_1ntR_b\right)//Đ_2\)
\(R_1=\dfrac{U_{Đ1}^2}{P_{Đ1}}=\dfrac{10^2}{2}=50\Omega;I_{Đ1đm}=\dfrac{P_{Đ1}}{U_{Đ1}}=\dfrac{2}{10}=0,2A\)
\(R_2=\dfrac{U^2_{Đ2}}{P_{Đ2}}=\dfrac{12^2}{3}=48\Omega;I_{Đ2đm}=\dfrac{P_{Đ2}}{U_{Đ2}}=\dfrac{3}{12}=0,25A\)
Để đèn 1 sáng bình thường \(\Rightarrow I_b=I_{Đ1đm}=0,2A\)
\(R_{Đ1+b}=\dfrac{12}{0,2}=60\Omega\)
\(R_b=60-R_{Đ1}=60-50=10\Omega\)


Bài 2:
\(A=2+2^2+2^3+...+2^{60}\)
\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{59}+2^{60}\right)\)
\(A=2\cdot\left(1+2\right)+2^3\cdot\left(1+2\right)+...+2^{59}\cdot\left(1+2\right)\)
\(A=2\cdot3+2^3\cdot3+...+2^{59}\cdot3\)
\(A=3\cdot\left(2+2^3+...+2^{59}\right)\) ⋮ 3
Vậy: A ⋮ 3
_____________
\(A=2+2^2+...+2^{60}\)
\(A=\left(2+2^2+2^3\right)+\left(2^4+2^5+2^6\right)+...+\left(2^{58}+2^{59}+2^{60}\right)\)
\(A=2\cdot\left(1+2+4\right)+2^4\cdot\left(1+2+4\right)+...+2^{58}\cdot\left(1+2+4\right)\)
\(A=2\cdot7+2^4\cdot7+...+2^{58}\cdot7\)
\(A=7\cdot\left(2+2^4+....+2^{58}\right)\) ⋮ 7
Vậy: A ⋮ 7
___________________
\(A=2+2^2+...+2^{60}\)
\(A=\left(2+2^3\right)+\left(2^2+2^4\right)+...+\left(2^{58}+2^{60}\right)\)
\(A=2\cdot\left(1+4\right)+2^2\cdot\left(1+4\right)+...+2^{58}\cdot\left(1+4\right)\)
\(A=2\cdot5+2^2\cdot5+...+2^{58}\cdot5\)
\(A=5\cdot\left(2+2^2+...+2^{58}\right)\) ⋮ 5
Vậy: A ⋮ 5


Lời giải:
Nếu $n$ chia hết cho $3$. Đặt $n=3k$ với $k$ tự nhiên.
Khi đó: $A=10^n+18n-1=10^{3k}+18.3k-1=1000^k+54k-1$
Có:
$1000\equiv 1\pmod {27}\Rightarrow 1000^k\equiv 1^k\equiv 1\pmod {27}$
$54k\equiv 0\pmod {27}$
$\Rightarrow 1000^k+54k-1\equiv 1+0-1\equiv 0\pmod {27}$
Hay $A\equiv 0\pmod {27}(1)$
Nếu $n$ chia $3$ dư $1$. Đặt $n=3k+1$ với $k$ tự nhiên.
Khi đó:
$A=10^{3k+1}+18(3k+1)-1=1000^k.10+54k+17$
$\equiv 1^k.10+0+17=27\equiv 0\pmod {27}(2)$
Nếu $n$ chia $3$ dư $2$. Đặt $n=3k+2$ với $k$ tự nhiên.
Khi đó:
$A=10^{3k+2}+18(3k+2)-1=1000^k.100+54k+35$
$\equiv 1^k.100+0+35=135\equiv 0\pmod {27}(3)$
Từ $(1); (2); (3)\Rightarrow A\vdots 27$ với mọi $n$ tự nhiên.

refer
- Tác dụng về nhiệt: đèn dây tóc, bàn ủi,... - Tác dụng phát sáng: đèn huỳnh quang, đèn LED,... - Tác dụng sinh lý: châm cứu, sốc điện tim,...
bạn tham khảo nha
Các tác dụng của dòng điện là :
- Tác dụng về nhiệt: đèn dây tóc, bàn ủi,...
- Tác dụng phát sáng: đèn huỳnh quang, đèn LED,...
- Tác dụng từ: quạt điện, chuông điện,....
- Tác dụng hóa học: mạ vàng,...
- Tác dụng sinh lý: châm cứu, sốc điện tim,...

\(\dfrac{3}{5}\)\(x\) - \(\dfrac{11}{5}\) = \(\dfrac{-3}{14}\) : \(\dfrac{5}{7}\)
\(\dfrac{3}{5}\)\(x\) - \(\dfrac{11}{5}\) = - \(\dfrac{3}{10}\)
\(\dfrac{3}{5}\)\(x\) = - \(\dfrac{3}{10}\) + \(\dfrac{11}{5}\)
\(\dfrac{3}{5}\)\(x\) = \(\dfrac{19}{10}\)
\(x\) = \(\dfrac{19}{10}\) : \(\dfrac{3}{5}\)
\(x\) = \(\dfrac{19}{6}\)
\(\dfrac{3}{5}x-\dfrac{11}{5}=-\dfrac{3}{14}:\dfrac{5}{7}\)
\(\Rightarrow\dfrac{3}{5}x-\dfrac{11}{5}=-\dfrac{3}{14}\cdot\dfrac{7}{5}\)
\(\Rightarrow\dfrac{3}{5}x-\dfrac{11}{5}=-\dfrac{3}{10}\)
\(\Rightarrow\dfrac{3}{5}x=-\dfrac{3}{10}+\dfrac{11}{5}\)
\(\Rightarrow\dfrac{3}{5}x=\dfrac{19}{10}\)
\(\Rightarrow x=\dfrac{19}{10}:\dfrac{3}{5}\)
\(\Rightarrow x=\dfrac{19}{6}\)

1 being
2 to do
3 moving
4 to do
5 take/going
6 leaving
7 repairing
8 playing
9 to use
10 speaking









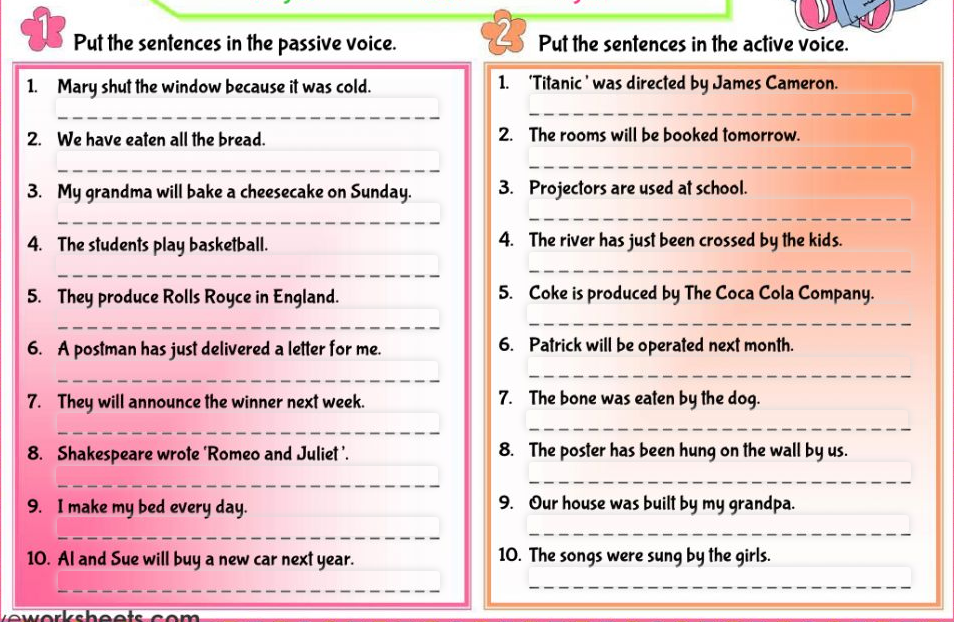 Giúp mình với ạ, mình cảm ơnnn
Giúp mình với ạ, mình cảm ơnnn


