Cho nửa đường tròn tâm O đường kính BC, lấy điểm A trên nửa đường tròn sao cho AB < AC.trên bờ mặt phẳng AC không chứa B vẽ hình vuông ACDE.Đường chéo Ab cắt nửa dường tròn tại một điểm M.Tia BM cắt DE tại F.CMRa)Tam giác BMC cân vuôngb)Tứ giác BEFC là tứ giác nội tiếpc)CF là tiếp tuyền của đường tròN...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính BC, lấy điểm A trên nửa đường tròn sao cho AB < AC.trên bờ mặt phẳng AC không chứa B vẽ hình vuông ACDE.Đường chéo Ab cắt nửa dường tròn tại một điểm M.Tia BM cắt DE tại F.CMR
a)Tam giác BMC cân vuông
b)Tứ giác BEFC là tứ giác nội tiếp
c)CF là tiếp tuyền của đường tròN (O)
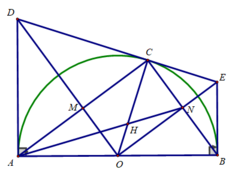
a) Tứ giác ACDE là hình vuông (gt).
\(\Rightarrow\) \(\widehat{DAE}=\widehat{DAC}\) (Tính chất hình vuông).
Xét tứ giác AMCB:
\(A;M;C;B\in\left(O\right)\left(gt\right).\)
\(\Rightarrow\) Tứ giác AMCB nội tiếp (O).
\(\Rightarrow\) \(\left\{{}\begin{matrix}\widehat{MCB}=\widehat{DAE}.\\\widehat{MBC}=\widehat{DAC}.\end{matrix}\right.\)
Mà \(\widehat{DAE}=\widehat{DAC}\left(cmt\right).\)
\(\Rightarrow\widehat{DAE}=\widehat{DAC}=\widehat{MCB}=\widehat{MBC}.\)
Xét (O):
\(M\in\left(O\right)\left(gt\right).\)
BC là đường kính (gt).
\(\Rightarrow\widehat{BMC}=90^o\) (Góc nội tiếp chắn nửa đường tròn).
Xét \(\Delta BMC:\)
\(\widehat{MCB}=\widehat{MBC}\left(cmt\right).\)
\(\Rightarrow\text{}\Delta BMC\) cân tại M.
Mà \(\widehat{BMC}=90^o\left(cmt\right).\)
\(\Rightarrow\text{}\Delta BMC\) vuông cân tại M.
b) Tứ giác ACDE là hình vuông (gt).
\(\Rightarrow\) \(\widehat{AED}=\widehat{EDC}=\widehat{DCA}=\widehat{CAE}=90^o\) (Tính chất hình vuông).
Xét tứ giác FDCM:
\(\widehat{FMC}+\widehat{FDC}=90^o+90^o=180^o.\)
Mà 2 góc ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác FDCM nội tiếp đường tròn.
\(\Rightarrow\widehat{FCM}=\widehat{FDM}.\)
Mà \(\widehat{FDM}+\widehat{EAD}=90^o\) (2 góc phụ nhau).
\(\Rightarrow\widehat{FCM}+\widehat{EAD}=90^o.\)
Lại có \(\widehat{EAD}=\widehat{MCB}\left(cmt\right).\)
\(\Rightarrow\widehat{FCM}+\widehat{MCB}=90^o.\\ \Rightarrow\widehat{FCB}=90^o.\)
Xét tứ giác BEFC:
\(\widehat{FCB}+\widehat{FEB}=90^o+90^o=180^o.\)
Mà 2 góc ở vị trí đối nhau.
\(\Rightarrow\) Tứ giác BEFC nội tiếp đường tròn.
c) Xét (O):
BC là đường kính (gt).
\(FC\perp BC\left(\widehat{FCB}=90^o\right).\)
\(\Rightarrow\) FC là là tiếp tuyền của đường tròn (O).