Cho tứ diện ABCD có AB = AC = AD và \(\widehat{BAC}=\widehat{BAD}=60^o\) ; \(\widehat{CAD}=90^o\).
Gọi I và J lần lượt là trung điểm của AB và CD. Hãy xác định góc giữa cặp vectơ AB và IJ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)

Trên tia đối của DC lấy I sao cho DI = CB
Khi đó: \(CB+CD=DI+CD=IC\)
Tứ giác ABCD có: \(\widehat{BAD}+\widehat{BCD}=60^0+120^0=180^0\)
\(\Rightarrow\widehat{ADC}+\widehat{ABC}=180^0\)
Mà \(\widehat{ADC}+\widehat{ADI}=180^0\Rightarrow\widehat{ABC}=\widehat{ADI}\)
\(\Delta BAD:AB=AD,\widehat{BAD}=60^0\Rightarrow\Delta BAD\) đều
\(\Rightarrow\widehat{BAD}=60^0\)
\(\Delta ABC=\Delta ADI\left(c.g.c\right)\Rightarrow\hept{\begin{cases}\widehat{BAC}=\widehat{DAI}\\AC=AI\end{cases}}\)
\(\widehat{CAI}=\widehat{CAD}+\widehat{DAI}=\widehat{CAD}+\widehat{BAC}=\widehat{BAD}=60^0\)
Tam giác ACI đều nên AC = AI = CI
Mà \(CB+CD=IC\Rightarrow CA=CB+CD\)

Đáp án D
Phương pháp
Sử dụng công thức tính nhanh thể tích khối tứ diện biết ba cạnh và ba góc cùng xuất phát từ một đỉnh:
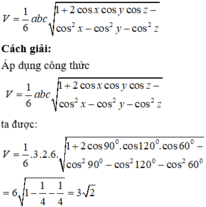
Ủa bạn, đề hỏi góc giữa vectơ AB và IJ cơ mà?