Cho ∆ABC có 3 góc nhọn có AC >AB, đường cao AD, BE, CF cắt nhau tại H.1) Chứng minh rằng: 4 điểm A, E, D, B cùng thuộc một đường tròn (gọi là đường tròn tâm O).2) Chứng minh rằng: ∆HDE đồng dạng ∆HBA3) Gọi K là giao điểm của DE và AB. Chứng minh rằng: ∆ KDB đồng dạng ∆KAE. Từ đó suy ra KD.KE = KB.AK4) Chứng minh rằng: H cách đều 3 đoạn thẳng EF, DE, DF. hộ e zới ạ tks...
Đọc tiếp
Cho ∆ABC có 3 góc nhọn có AC >AB, đường cao AD, BE, CF cắt nhau tại H.
1) Chứng minh rằng: 4 điểm A, E, D, B cùng thuộc một đường tròn (gọi là đường tròn tâm O).
2) Chứng minh rằng: ∆HDE đồng dạng ∆HBA
3) Gọi K là giao điểm của DE và AB. Chứng minh rằng: ∆ KDB đồng dạng ∆KAE. Từ đó suy ra KD.KE = KB.AK
4) Chứng minh rằng: H cách đều 3 đoạn thẳng EF, DE, DF.
hộ e zới ạ tks mn
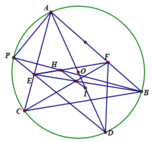
1) Xét tứ giác AEBD:
\(\widehat{AEB}=\widehat{ADB}=90^o\left(BE\perp AE;AD\perp BD\right).\)
\(\Rightarrow\) Tứ giác AEBD nội tiếp đường tròn (dhnb).
\(\Rightarrow\) A; E; B; D cùng thuộc một đường tròn (O).
2) Tứ giác AEBD nội tiếp đường tròn (cmt).
\(\Rightarrow\) \(\widehat{ADE}=\widehat{ABE}.\)
hay \(\widehat{HDE}=\widehat{HBA}.\)
Xét ∆ HDE và ∆ HBA:
\(\widehat{HDE}=\widehat{HBA}\left(cmt\right).\)
\(\widehat{EHD}=\widehat{AHB}\) (Đối đỉnh).
\(\Rightarrow\Delta HDE\sim\Delta HBA\left(g-g\right).\)
3) Tứ giác AEBD nội tiếp đường tròn (cmt).
\(\Rightarrow\widehat{KDB}=\widehat{KAE}.\)
Xét ∆ KDB và ∆ KAE:
\(\widehat{KDB}=\widehat{KAE}\left(cmt\right).\)
\(\widehat{DKB}chung.\)
\(\Rightarrow\Delta KDB\sim\Delta KAE\left(g-g\right).\)
\(\Rightarrow\dfrac{KD}{KA}=\dfrac{KB}{KE}\) (2 cạnh tương ứng tỉ lệ).
\(\Rightarrow KD.KE=KB=KA\left(đpcm\right).\)
1: Xét tứ giác AEDB có
\(\widehat{AEB}=\widehat{ADB}=90^0\)
Do đó: AEDB là tứ giác nội tiếp
2: Xét ΔHDE và ΔHBA có
\(\widehat{HDE}=\widehat{HBA}\)
\(\widehat{DHE}=\widehat{BHA}\)
Do đó: ΔHDE∼ΔHBA
3: Xét ΔKDB và ΔKAE có
\(\widehat{K}\) chung
\(\widehat{KDB}=\widehat{KAE}\)
Do đó: ΔKDB∼ΔKAE
Suy ra: KD/KA=KB/KE
hay \(KD\cdot KE=KA\cdot KB\)