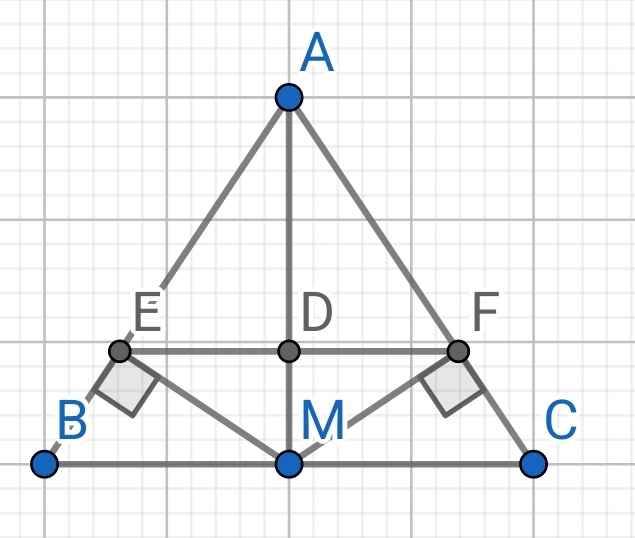
Cho ∆ABC.M là điểm nằm trong ∆ABC.Vẽ MD vuông góc BC tại D,ME vuông góc AC tại E,MF vuông góc AB tại F.Chứng minh rằng AF² + BD² + CE² = AE² + BF² + CD²
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
13 tháng 12 2023
a) Do M là trung điểm của BC (gt)
⇒ BM = CM
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆AMB và ∆AMC có:
AM là cạnh chung
AB = AC (cmt)
BM = CM (cmt)
⇒ ∆AMB = ∆AMC (c-c-c)
b) Sửa đề:
Chứng minh AM EF
Giải:
Gọi D là giao điểm của AM và EF
Do ∆AMB = ∆AMC (cmt)
⇒ ∠MAB = ∠MAC (hai góc tương ứng)
⇒ ∠MAE = ∠MAF
Xét hai tam giác vuông: ∆MAE và ∆MAF có:
AM là cạnh chung
∠MAE = ∠MAF (cmt)
⇒ ∆MAE = ∆MAF (cạnh huyền - góc nhọn)
⇒ AE = AF (hai cạnh tương ứng)
Do ∠MAE = ∠MAF (cmt)
⇒ ∠DAE = ∠DAF
Xét ∆ADE và ∆ADF có:
AD là cạnh chung
∠DAE = ∠DAF (cmt)
AE = AF (cmt)
⇒ ∆ADE = ∆ADF (c-g-c)
⇒ ∠ADE = ∠ADF (hai góc tương ứng)
Mà ∠ADE + ∠ADF = 180⁰ (kề bù)
⇒ ∠ADE = ∠ADF = 180⁰ : 2 = 90⁰
⇒ AD ⊥ EF
8 tháng 1 2022
a: Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó: ΔAEB vuông tại E
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{BIF}=180^0\)
Do đó: BEFI là tứ giác nội tiếp
b: Xét ΔACE và ΔAFC có
\(\widehat{CAF}\) chung
\(\widehat{AEC}=\widehat{ACF}\)
Do đó: ΔACE\(\sim\)ΔAFC
Suy ra: \(\dfrac{AE}{AC}=\dfrac{AC}{AF}\)
hay \(AE\cdot AF=AC^2\)
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 1 2022
Do E thuộc đường tròn \(\Rightarrow\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\widehat{AEB}=90^0\)
Lại có \(\widehat{FIB}=90^0\) (do \(CD\perp AB\) tại I)
\(\Rightarrow\) E và I cùng nhìn BF dưới 1 góc vuông
\(\Rightarrow\) Tứ giác BEFI nội tiếp đường tròn đường kính BF
b.
Xét hai tam giác vuông AIF và AEB có: góc \(\widehat{IAF}\) chung
\(\Rightarrow\Delta_VAIF\sim\Delta_VAEB\left(g.g\right)\Rightarrow\dfrac{AI}{AE}=\dfrac{AF}{AB}\Rightarrow AI.AB=AE.AF\) (1)
Mặt khác \(\widehat{ACB}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow\Delta ACB\) vuông tại C
Áp dụng hệ thức lượng cho tam giác vuông ACB với đường cao CI:
\(AC^2=AI.AB\) (2)
(1);(2) \(\Rightarrow AE.AF=AC^2\)
- Xét tam giác AFM vuông tại F có:
AF2+FM2=AM2 (định lí Py-ta-go).
=>FM2=AM2-AF2. (1)
- Xét tam giác BFM vuông tại F có:
BF2+FM2=BM2 (định lí Py-ta-go).
=>FM2=BM2-BF2 (2)
- Từ (1) và (2) suy ra: AM2-AF2=BM2-BF2 (7)
- Xét tam giác MBD vuông tại D có:
MD2+BD2=BM2 (định lí Py-ta-go).
=>MD2=BM2-BD2 (3)
- Xét tam giác MCD vuông tại D có:
MD2+DC2=MC2 (định lí Py-ta-go).
=>MD2=MC2-DC2 (4)
- Từ (3) và (4) suy ra: BM2-BD2=MC2-DC2 (8)
- Xét tam giác MEC vuông tại E có:
ME2+EC2=MC2 (định lí Py-ta-go).
=>ME2=MC2-EC2 (5)
- Xét tam giác MEA vuông tại E có:
ME2+AE2=MA2 (định lí Py-ta-go).
=>ME2=MA2-AE2 (6)
- Từ (5) và (6) suy ra: MC2-EC2=MA2-AE2 (9)
- Từ (7),(8),(9) suy ra:
AM2-AF2+BM2-BD2+MC2-EC2=BM2-BF2+MC2-DC2+MA2-AE2
=>-AF2-BD2-EC2=-BF2-DC2-AE2
=>AF2+BD2+EC2=BF2+DC2+AE2