Cho ▲ABC có AB= 3cm AC=6cm ,góc A=120° kẻ phân giác AD tính AD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
1
M
3 tháng 5 2018
Qua D kẻ DE // AB ( E \(\in\)AB )
Vì AD là phân giác góc A của \(\Delta ABC\):
\(\Rightarrow\)\(\frac{DC}{DB}=\frac{AC}{AB}\)
\(\Rightarrow\) \(\frac{DC}{DB+DC}=\frac{AC}{AB+AC}\)hay \(\frac{DC}{BC}=\frac{6}{3+6}\)\(\Leftrightarrow\)\(\frac{DC}{BC}=\frac{2}{3}\)(1)
Ta có : AB là phân giác góc A \(\Rightarrow\)\(\widehat{A_1}=\widehat{A_2}=\frac{\widehat{BAC}}{2}=\frac{120}{2}=60^0\)
Mà \(\widehat{A_1}=\widehat{D_1}=60^0\)( so le trong , DE // AB )
\(\Rightarrow\widehat{A_2}=\widehat{D_1}=60^0\Rightarrow\)\(\Delta ADE\)đều
\(\Rightarrow\)AD = DE
Vì DE // AB ( cách dựng )
Xét \(\Delta ABC\)theo hệ quả định lý Ta-lét ta có:\(\frac{DE}{AB}=\frac{DC}{BC}\)(2)
Thế (1) vào (2) ta được :\(\frac{DE}{AB}=\frac{2}{3}\)hay \(\frac{DE}{3}=\frac{2}{3}\)
\(\Rightarrow DE=\frac{2.3}{3}=2\left(cm\right)\)
\(\Rightarrow AD=2\left(cm\right)\)( AD=DE chứng minh trên )
QN
0
10 tháng 3 2023
11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)
TT
1
CM
2 tháng 4 2017
Theo tính chất tia phân giác của góc ta có:
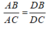
Suy ra:
Chọn đáp án D
CT
1
20 tháng 7 2018
Áp dụng Pitago ta có : BC = 10
Áp dụng tính chất của tia phân giác ta có : BD/DC = AB/AC = 3/4
=> BD/BC = 3/7 => BD = 30/7 cm, CD = 40/7 cm
HD // AC => HD / AC = BD / BC
=> HD = 30/70.8 = 24/7
Do góc HAD = 45 độ => T/g HAD vuông cân => AD^2 = 1152/49 => AD = \(\frac{24\sqrt{2}}{7}\)cm
NT
1
10 tháng 7 2021
Vì \(AC\perp AB;HD\perp AB\Rightarrow AC//HD\)
Áp dụng hệ quả Ta lét ta có : \(\frac{BD}{BC}=\frac{HD}{AC}\)(*)
Vì AD là đường phân giác ^A nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Lại có : \(BC^2=AB^2+AC^2=36+64=100\Rightarrow BC=10\)cm
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{10}{14}=\frac{5}{7}\)
\(\Rightarrow DC=\frac{5}{7}AC=\frac{5}{7}.8=\frac{40}{7}\)cm ; \(BD=\frac{5}{7}AB=\frac{5}{7}.6=\frac{30}{7}\)cm
Thay vào (*) ta được : \(\frac{\frac{30}{7}}{10}=\frac{HD}{8}\Rightarrow10HD=\frac{240}{7}\Rightarrow HD=\frac{24}{7}\)cm
Có : \(\frac{BH}{AB}=\frac{HD}{AC}\)( hệ quả Ta lét ) \(\Rightarrow BH=\frac{AB.HD}{AC}=\frac{6.\frac{24}{7}}{8}=\frac{18}{7}\)cm
\(\Rightarrow AH=AB-BH=6-\frac{18}{7}=\frac{24}{7}\)cm
Áp dụng định lí Pytago tam giác AHD vuông tại H ta có :
\(AD^2=AH^2+HD^2=\left(\frac{24}{7}\right)^2+\left(\frac{24}{7}\right)^2=2\left(\frac{24}{7}\right)^2\)
\(\Rightarrow AD=\frac{24\sqrt{2}}{7}\)cm o.O bạn check lại xem nhé
kẻ đường BH vuông góc xuống AC
ta có bah=60 tính đc HA,BH
theo tính chất đường phân giác ta có AB/AC=BD/DC=1/2 NÊN DC/BC=2/3
KẺ DK vuông góc với AC ta tính được DK và HK theo các tgiac đồng dạng
ta lại tính đc AK=HK-AH
biết DK và AK áp dụng pitago tìm đc ad
ĐS:2