Câu 7 ạ 🥲
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(lim\dfrac{2\sqrt{7n^2-2n}}{3n+2}=lim\dfrac{2\sqrt{n^2\left(7-\dfrac{2}{n}\right)}}{3n+2}=lim\dfrac{2n\sqrt{7-\dfrac{2}{n}}}{n\left(3+\dfrac{2}{n}\right)}\)
\(=lim\dfrac{2\sqrt{7-\dfrac{2}{n}}}{3+\dfrac{2}{n}}=\dfrac{2\sqrt{7}}{3}\) \(=\dfrac{a\sqrt{7}}{b}\)
Suy ra : a/b = 2/3 => a - b = -1

\(\dfrac{x-1}{x+2}+\dfrac{6x}{x^2-4}=\dfrac{x+1}{2-x}\left(dkxd:x\ne\pm2\right)\)
\(\Leftrightarrow\dfrac{x-1}{x+2}+\dfrac{6x}{\left(x-2\right)\left(x+2\right)}=-\dfrac{x+1}{x-2}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)+6x+\left(x+1\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=0\)
\(\Leftrightarrow x^2-2x-x+2+6x+x^2+2x+x+2=0\)
\(\Leftrightarrow2x^2+6x+4=0\)
\(\Leftrightarrow2x^2+2x+4x+4=0\)
\(\Leftrightarrow2x\left(x+1\right)+4\left(x+1\right)=0\)
\(\Leftrightarrow\left(2x+4\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+4=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\left(ktm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-1\right\}\)

1 If we continue polluting the air, the environment will be affected seriously
2 If we don't stop damaging birds' homes, there will be fewer birds left
3 If we continue polluting the water, there will be more disease in people and animals
4 If we keep polluting the land, the soil will not be safe enough for us to grow food in
5 If we use public transportation when we need, there will be less air pollution
12 Daniel signs up for a clean-up campaign so that he can join in it
13 People in my neighborhood clean the park up so that their children will have a nice place to play
14 Almost all the students in my school plant trees so that they can have much fresher air

3:
a: Xét ΔAEH vuông tại E và ΔADC vuông tại D có
góc EAH chung
=>ΔAEH đồng dạng với ΔADC
=>AE/AD=AH/AC
=>AE*AC=AH*AD
b: Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
góc C chung
=>ΔCEB đồng dạng với ΔCDA
=>CE/CD=CB/CA
=>CE*CA=CD*CB
c: S ABC=1/2*BC*AD=9cm2


e: \(\dfrac{x^2+3x+9}{x^3+4x^2+4x}\cdot\dfrac{x^2+2x}{x^3-27x}\)
\(=\dfrac{x^2+3x+9}{x\left(x^2+4x+4\right)}\cdot\dfrac{x\left(x+2\right)}{x\left(x^2-27\right)}\)
\(=\dfrac{x^2+3x+9}{\left(x+2\right)^2}\cdot\dfrac{x+2}{x\left(x^2-27\right)}\)
\(=\dfrac{\left(x^2+3x+9\right)}{\left(x+2\right)\cdot x\left(x^2-27\right)}\)
f: \(\dfrac{2x^2+4xy+2y^2}{5x-5y}\cdot\dfrac{15x-15y}{2x^3+2y^3}\)
\(=\dfrac{2\left(x^2+2xy+y^2\right)}{5\left(x-y\right)}\cdot\dfrac{15\left(x-y\right)}{2\left(x^3+y^3\right)}\)
\(=\dfrac{\left(x+y\right)^2}{1}\cdot\dfrac{3}{\left(x+y\right)\left(x^2-xy+y^2\right)}\)
\(=\dfrac{3\left(x+y\right)}{x^2-xy+y^2}\)
g: \(\dfrac{x^3-4x}{x^2-7x+12}\cdot\dfrac{x-4}{x^2-2x}\)
\(=\dfrac{x\left(x^2-4\right)}{\left(x-3\right)\left(x-4\right)}\cdot\dfrac{x-4}{x\left(x-2\right)}\)
\(=\dfrac{x^2-4}{\left(x-3\right)\left(x-2\right)}=\dfrac{\left(x-2\right)\left(x+2\right)}{\left(x-3\right)\left(x-2\right)}=\dfrac{x+2}{x-3}\)

m: \(=x^m\cdot x^2-x^m=x^m\left(x^2-1\right)=x^m\left(x-1\right)\left(x+1\right)\)
n: \(=5\cdot x^m\cdot x^2+10x^2\)
\(=5x^2\left(x^m+2\right)\)
o: \(=5x\left(x-2y\right)+2\left(x-2y\right)^2\)
\(=\left(x-2y\right)\left(5x+2x-4y\right)\)
=(x-2y)(7x-4y)
p: \(=7x\left(y-4\right)^2+\left(y-4\right)^3\)
\(=\left(y-4\right)^2\cdot\left(7x+y-4\right)\)
q: \(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\)
\(=\left(4x-8\right)\left(x^2+6-x-7\right)-9\left(4x-8\right)\)
\(=\left(4x-8\right)\left(x^2-x-10\right)\)
\(=4\left(x-2\right)\left(x^2-x-10\right)\)
m) \(x^{m+2}-x^m\)
\(=x^m\cdot x^2-x^m\)
\(=x^m\left(x^2-1\right)\)
\(=x^m\left(x^2-1^2\right)\)
\(=x^m\left(x-1\right)\left(x+1\right)\)
n) \(5x^{m+2}+10x^2\)
\(=5x^m\cdot x^2+10x^2\)
\(=5x^2\cdot x^m+10x^2\)
\(=5x^2\left(x^m+2\right)\)
o) \(5x\left(x-2y\right)+2\left(2y-x\right)^2\)
\(=5x\left(x-2y\right)+2\left(x-2y\right)^2\)
\(=\left(x-2y\right)\left[5x+2\left(x-2y\right)\right]\)
\(=\left(x-2y\right)\left(5x+2x-4y\right)\)
\(=\left(x-2y\right)\left(7x-4y\right)\)
p) \(7x\left(y-4\right)^2-\left(4-y\right)^3\)
\(=7x\left(4-y\right)^2-\left(4-y\right)^3\)
\(=\left(4-y\right)^2\left[7x-\left(4-y\right)\right]\)
\(=\left(4-y\right)^2\left(7x-4+y\right)\)
q) \(\left(4x-8\right)\left(x^2+6\right)-\left(4x-8\right)\left(x+7\right)+9\left(8-4x\right)\)
\(=4\left(x-2\right)\left(x^2+6\right)-4\left(x-2\right)\left(x+7\right)-36\left(x-2\right)\)
\(=4\left(x-2\right)\left[\left(x^2+6\right)-\left(x+7\right)-9\right]\)
\(=4\left(x-2\right)\left(x^2+6-x-7-9\right)\)
\(=4\left(x-2\right)\left(x^2-x-10\right)\)


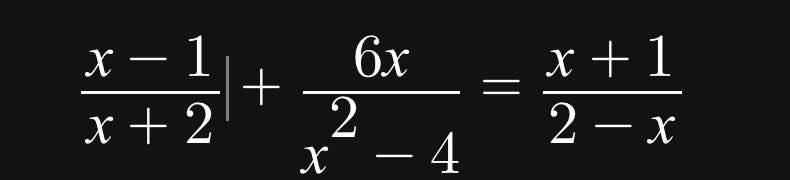




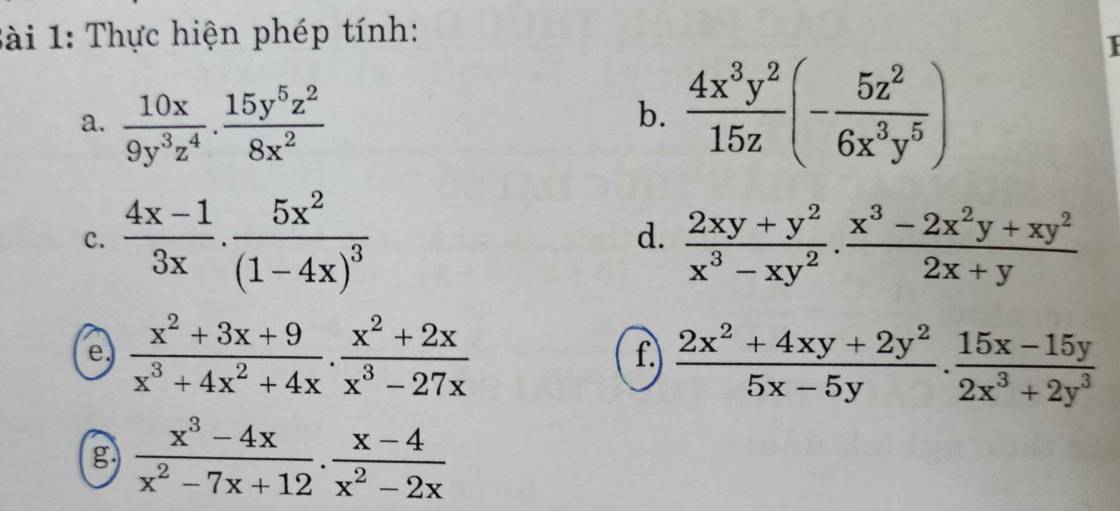
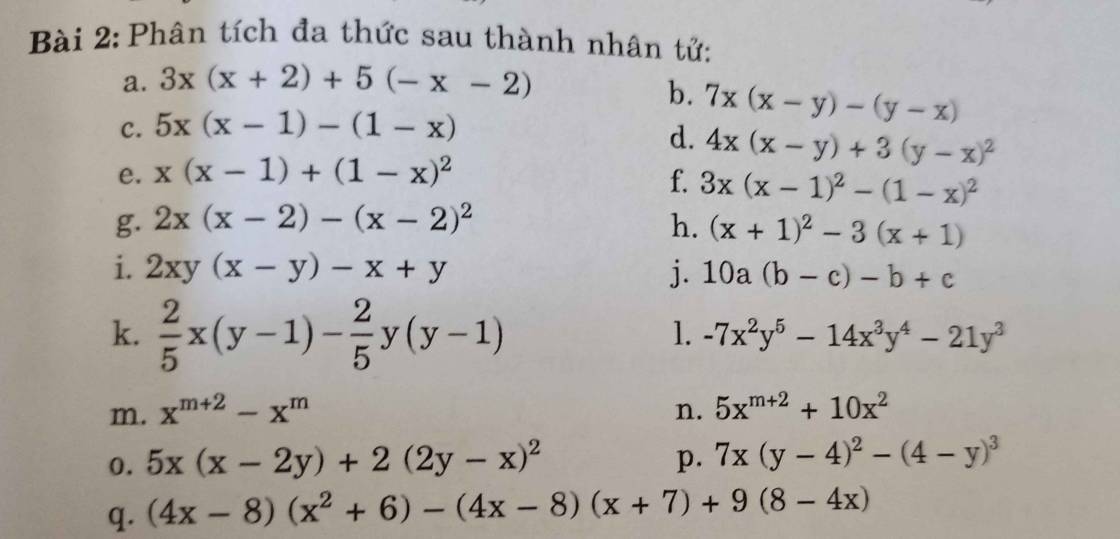
Câu 7:
Theo đề, ta có:
\(\left\{{}\begin{matrix}a\sqrt{2}+b=2\\a+b=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\left(\sqrt{2}-1\right)=2-\sqrt{2}\\a+b=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\sqrt{2}\\b=0\end{matrix}\right.\)