Tìm x,y biết xy+3x-2y=11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
L
26 tháng 10 2019
\(a)xy+3x-2y=11\)
\(\Leftrightarrow xy+3x-2y-6=5\)
\(\Leftrightarrow x\left(y+3\right)-2\left(y+3\right)=5\)
\(\Leftrightarrow\left(y+3\right)\left(x-2\right)=5\)
\(\Leftrightarrow\hept{\begin{cases}y+3=-1\\x-2=-5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-4\\x=-3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+3=1\\x-2=5\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-2\\x=7\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+3=-5\\x-2=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-8\\x=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+3=5\\x-2=1\end{cases}}\Leftrightarrow\hept{\begin{cases}y=2\\x=3\end{cases}}\)
L
26 tháng 10 2019
\(b)2x^2-2xy+x-y=12\)
\(\Leftrightarrow2x\left(x-y\right)+\left(x-y\right)=12\)
\(\Leftrightarrow\left(x-y\right)\left(2x+1\right)=12\)
\(\Rightarrow\left(x-y\right);\left(2x+1\right)\inƯ\left(12\right)\)
\(\RightarrowƯ\left(12\right)\in\left\{-1;1;-2;2;-3;3;-4;4;-6;6;-12;12\right\}\)
Vì 2x+1 luôn lẻ
\(\Rightarrow2x+1\in\left\{-1;1;-3;3\right\}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=-1\\x-y=-12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=11\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=1\\x-y=12\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\y=-12\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=-3\\x-y=-4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2\\y=2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+1=3\\x-y=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=1\\y=-3\end{cases}}\)
25 tháng 4 2016
xy + 3x-2y=11
<=> x(y+3)-2(y+3)=5
<=>(x-2)(y+3)=5
suy ra (x-2) và (y+3) là các ước nguyên của 5.
Th1. x-2=1 <=>x=3
.......y+3=5 <=> y=2
Th2 x-2=-1 <=> x=1
.......y+3=-5 <=> y= -8
Th3. x-2=5 <=> x=7
.......y+3=1 <=> y= -2
Th4. x-2= -5 <=> x= -3
.......y+3= -1 <=> y= -4
Vậy (x,y) = (3, 2); (1, -8); (7, -2); (-3, -4)
25 tháng 4 2016
xy + 3x-2y=11
<=> x(y+3)-2(y+3)=5
<=>(x-2)(y+3)=5
suy ra (x-2) và (y+3) là các ước nguyên của 5.
Th1. x-2=1 <=>x=3
.......y+3=5 <=> y=2
Th2 x-2=-1 <=> x=1
.......y+3=-5 <=> y= -8
Th3. x-2=5 <=> x=7
.......y+3=1 <=> y= -2
Th4. x-2= -5 <=> x= -3
.......y+3= -1 <=> y= -4
Vậy (x,y) = (3, 2); (1, -8); (7, -2); (-3, -4)
VP
1
HA
12 tháng 2 2020
\(xy+3x-7y=21\)
\(x\left(3+y\right)-7y=21\)
\(x\left(3+y\right)-7y-21=0\)
\(x\left(3+y\right)-7\left(y+3\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(y+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-7=0\\y+3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=7\\y=-3\end{cases}}}\)
vậy x=7 và y=-3
NT
2
17 tháng 5 2016
a) \(xy+3x-2y-11=0\)
\(x\left(y+3\right)-2y-6-5=0\)
\(x\left(y+3\right)-2\left(y+3\right)=5\)
\(\left(x-2\right)\left(y+3\right)=5\)
\(x-2;y+3\in U\left(5\right)\)
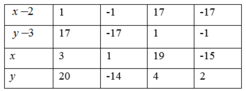
| x-2 | 1 | -1 | 5 | -5 |
| y+3 | 5 | -5 | 1 | -1 |
| x | 3 | 1 | 7 | -3 |
| y | 2 | -8 | -2 | -4 |
b) \(xy+2x+y+11=0\)
\(x\left(y+2\right)+y+2+9=0\)
\(x\left(y+2\right)+\left(y+2\right)=-9\)
\(\left(x+1\right)\left(y+2\right)=-9\)
\(x+1;y+2\in U\left(-9\right)\)
| x+1 | 1 | -1 | 3 | -3 | 9 | -9 |
| y+2 | -9 | 9 | -3 | 3 | -1 | 1 |
| x | 0 | -2 | 2 | -4 | 8 | -10 |
| y | -11 | 7 | -5 | 1 | -3 | -1 |
17 tháng 5 2016
a) $xy+3x-2y-11=0$$x\left(y+3\right)-2y-6-5=0$$x\left(y+3\right)-2\left(y+3\right)=5$$\left(x-2\right)\left(y+3\right)=5$$x-2;y+3\in U\left(5\right)$
b) $xy+2x+y+11=0$
$x\left(y+2\right)+y+2+9=0$$x\left(y+2\right)+\left(y+2\right)=-9$$\left(x+1\right)\left(y+2\right)=-9$$x+1;y+2\in U\left(-9\right)$
| x-2 | 1 | -1 | 5 | -5 | ||
| y+3 | 5 | -5 | 1 | -1 | ||
| x | 3 | 1 | 7 | -3 | ||
| y | 2 | -8 | -2 | -4 | ||
| x+1 | 1 | -1 | 3 | -3 | 9 | -9 |
| y+2 | -9 | 9 | -3 | 3 | -1 | 1 |
| x | 0 | -2 | 2 | -4 | 8 | -10 |
| y | -11 | 7 | -5 | 1 |
31 tháng 3 2016
xy+3x-2y=11
=>x(y+3)-2y-6=5
=>x(y+3)-(2y+6)=5
=>x(y+3)-2(y+3)=5
=>(x+2)(y+3)=5
Bạn kẻ bảng ra nha
27 tháng 11 2017
\(xy+3x-2y=11\)
\(\Leftrightarrow x\left(y+3\right)-2\left(y+3\right)=5\)
\(\Leftrightarrow\left(x-2\right)\left(y+3\right)=5\)
\(\Rightarrow\left(x-2\right);\left(y+3\right)\)là các ước nguyên của 5
\(Th1:x-2=1\Leftrightarrow x=3\)
\(y+3=5\Leftrightarrow y=3\)
\(Th2:x-2=-1\Leftrightarrow x=-1\)
\(y+3=-5\Leftrightarrow y=-8\)
\(Th3:x-2=5\Leftrightarrow x=7\)
\(y+3=1\Leftrightarrow y=1\)
\(Th4:x-2=-5\Leftrightarrow x=-3\)
\(y+3=-1\Leftrightarrow y=-4\)
Vậy: \(\left(x;y\right)\in\left\{3,2\right\};\left\{1,-8\right\};\left\{7;-2\right\};\left\{-3;-4\right\}\)
SA
0
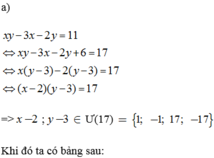
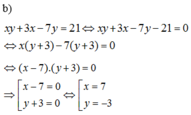
Đây là bài giải phương trình nghiệm nguyên, có thể giải theo hai cách như sau :
Cách 1 :
xy+3x-2y=11
<=>x(y+3) - 2y - 6 =11 - 6
<=>x(y+3) - 2(y+3) = 5
<=> (x-2)(y+3) = 5
=> x - 2 ; y +3 thuộc Ư(5)={±1;±5}
*x-2=1 => x=3
y+3=5 => y=2
*x-2= -1 => x=1
y+3= -5 => y= -8
*x-2=5 => x=7
y+3=1 => y= -2
*x-2= -5 => x= -3
y+3= -1 => y= -4
Vậy (x;y)=(3;2),(1;-8),(7;-2),(-3;-4)
Cách 2 :
xy +3x -2y = 11
x(y+3) = 2y+11
Nếu y= -3 thay vào phương trình, ta có 0x=5 (loại)
Nếu y khác -3 thì :
x= (2y+11) / (y+3)
x = 2 + 5/(y+3) (cái này là chia đa thức ý mà)
mà x thuộc Z
=> 5/(y+3) thuộc Z
=> y+3 thuộc Ư(5)={±1;±5}
=> y thuộc {-2;-4;2;-8}
mà x = 2 + 5/(y+3)
=> x thuộc {7;-3;1;3}
Vậy (x;y)=(3;2),(1;-8),(7;-2),(-3;-4)
xy + 3x-2y=11
<=> x(y+3)-2(y+3)=5
<=>(x-2)(y+3)=5
suy ra (x-2) và (y+3) là các ước nguyên của 5.
Th1. x-2=1 <=>x=3
.......y+3=5 <=> y=2
Th2 x-2=-1 <=> x=1
.......y+3=-5 <=> y= -8
Th3. x-2=5 <=> x=7
.......y+3=1 <=> y= -2
Th4. x-2= -5 <=> x= -3
.......y+3= -1 <=> y= -4
Vậy (x,y) = (3, 2); (1, -8); (7, -2); (-3, -4)