cho tam giác vuông abc vuông tại a co cac canh AB= 6 cm,AC= 8 cm, BC = 10 cm va ba nua hình tròn có đường kính lần lượt là AB, AC và BC . Tính S phần gạch chéo
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


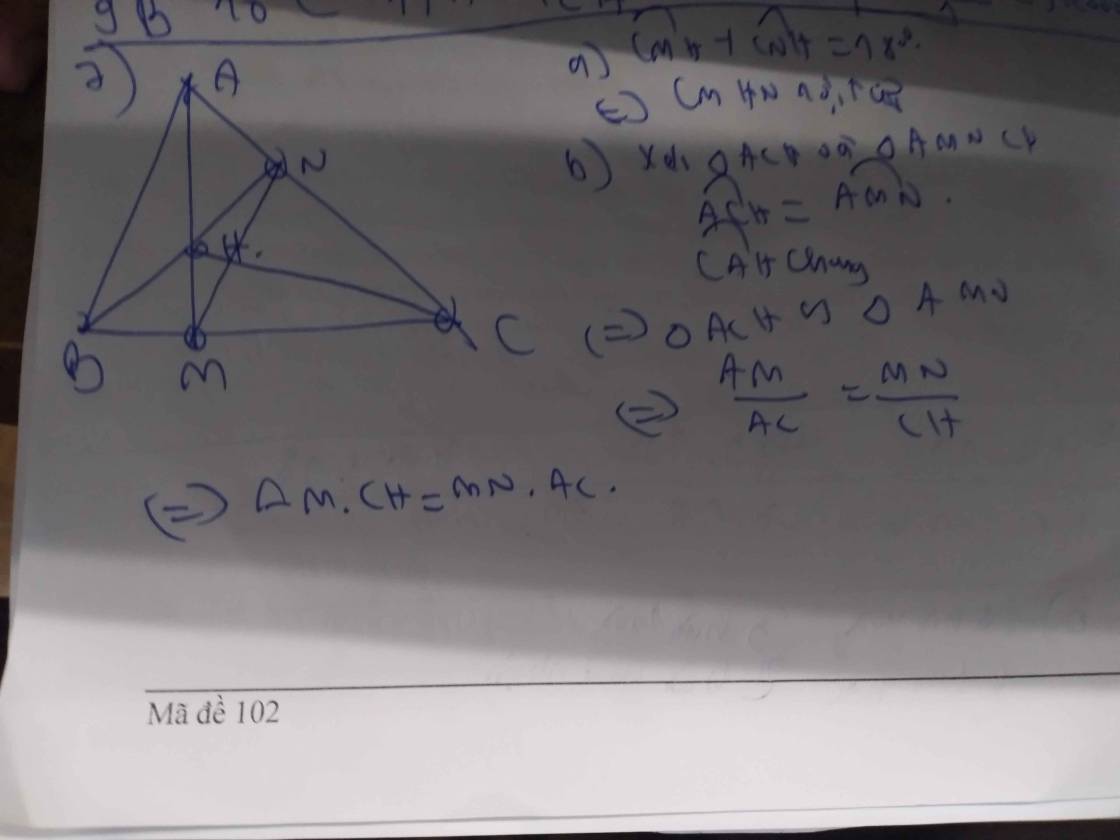
a: Xét (O) có
ΔMBC nội tiếp
BC là đường kính
Do đó: ΔMBC vuông tại M
Xét (O) có
ΔNBC nội tiếp
BC là đường kính
Do đó:ΔNBC vuông tại N
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH⊥BC tại K
b: Xét ΔANB vuông tại N và ΔAMC vuông tại M có
\(\widehat{MAC}\) chung
Do đó: ΔANB∼ΔAMC
Suy ra: AN/AM=AB/AC
hay \(AN\cdot AC=AB\cdot AM\)

diện tích hình tròn có đường kính là 5 cm là:5:2*5:2*3,14=19,625(cm2).diện tích hình tam giác là:3*4:2=6(cm2).diện tích hai ửa hình tròn nhỏ là:19,625 - 6=13,625(cm2).diện tích hình tròn lớn là:(3:2*3:2*3,14)+(4:2*4:2*3,14)=19,625(cm2).diện tích phần tô đậm là:19.625 -13,625=6(cm2)
)

Lời giải:
a/ Tứ giác $AEHF$ có 3 góc vuông: $\widehat{A}=\widehat{E}=\widehat{F}=90^0$ nên là hình chữ nhật.
$\Rightarrow AH=EF$
b/ $HF=AE$ (do $AEHF$ là hcn)
Xét tam giác $AEH$ và $AHB$ có:
$\widehat{A}$ chung
$\widehat{AEH}=\widehat{AHB}=90^0$
$\Rightarrow \triangle AEH\sim \triangle AHB$ (g.g)
$\Rightarrow \frac{AE}{AH}=\frac{AH}{AB}$
$\Rightarrow AE=\frac{AH^2}{AB}=\frac{AB^2-BH^2}{AB}=\frac{6^2-3,6^2}{6}=3,84$ (cm)