Giải chi tiết giúp mình đc ko...
Đọc tiếp
Giải chi tiết giúp mình đc ko ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HA
1
TC
21 tháng 12 2022
Thể tích của vật là
`V_v = V_2-V_1 =175-130=45cm^3=4,5*10^(-5)m^3`
Do vật chìm hoàn toàn trong nước nên
Lực đẩy Ác si met t/d lên vật là
`F_A = V_v * d_n =4,5*10^(-5) *10000 =0,45(N)`
khối lg của vật ngoài ko khí là
`m=P/10=(P_n +F_A )/10= (4,2+0,45)/10 =0,465(kg)`
khối lg riêng vật là
`D=m/V_v = (0,465)/(4,5*10^(-5))=~~ 10333,3(kg//m^3)`
K
2
5 tháng 11 2021
Áp dụng t/c dtsbn:
\(\dfrac{x-1}{8}=\dfrac{x+1}{12}=\dfrac{x+1-x+1}{12-8}=\dfrac{2}{4}=\dfrac{1}{2}\)
\(\Rightarrow x-1=\dfrac{1}{2}.8=4\Rightarrow x=4+1=5\)
25 tháng 11 2022
12(x-1)=8(x+1)
12x - 12 =8x + 8
12x - 8x = 8 +12
4x. = 20
x. = 20 :4
x. = 5
23 tháng 1 2022
\(B=\left(\dfrac{1}{9}-\dfrac{5}{7}\right)+\dfrac{3}{6}+\left(\dfrac{-12}{17}+\dfrac{-1}{2}\right)+\dfrac{5}{9}.\)
\(B=\dfrac{1}{9}-\dfrac{5}{7}+\dfrac{1}{2}-\dfrac{12}{17}-\dfrac{1}{2}+\dfrac{5}{9}=\left(\dfrac{1}{9}+\dfrac{5}{9}\right)+\left(\dfrac{1}{2}-\dfrac{1}{2}\right)-\dfrac{5}{7}-\dfrac{12}{17}=\dfrac{2}{3}-\dfrac{5}{7}-\dfrac{12}{17}=\dfrac{238-255-252}{357}=\dfrac{-269}{357}.\)
NB
2
20 tháng 4 2021
a) vì xoy+yoz=180 độ(2 góc kề bù)
=> yoz=180-xoy=130 độ
20 tháng 4 2021
vì oa là tia phân giác của xoy
=> xoa=aoy=xoy/2=50/2=25độ
vì ob .................................yoz
=> yob=boz=yoz/2=130/2=65độ
=> aob=aoy+yob=25+65=90độ
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
3 tháng 5 2023
\(a,33\times99=33\times100-33=3300-33=3267\\ b,25\%\times3+7\times\dfrac{1}{4}=\dfrac{1}{4}\times3+7\times\dfrac{1}{4}=\left(3+7\right)\times\dfrac{1}{4}=10\times\dfrac{1}{4}=\dfrac{5}{2}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
3 tháng 5 2023
\(c,\\ \dfrac{75}{100}\times16+4\times\dfrac{3}{4}\\ =\dfrac{3}{4}\times16+4\times\dfrac{3}{4}\\ =\left(16+4\right)\times\dfrac{3}{4}=20\times\dfrac{3}{4}=15\\ d,\\ 35\times99+35=35\times\left(99+1\right)=35\times100=3500\)
AN
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2023
a.
Hệ có nghiệm duy nhất khi:
\(\dfrac{m}{2}\ne\dfrac{1}{-1}\Rightarrow m\ne-2\)
b.
Hệ có vô số nghiệm khi:
\(\dfrac{1}{1}=\dfrac{m}{-1}=\dfrac{3}{3}\Rightarrow m=-1\)
c.
Hệ vô nghiệm khi:
\(\dfrac{2}{-4}=\dfrac{-1}{2}\ne\dfrac{-m}{4}\Rightarrow m\ne2\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
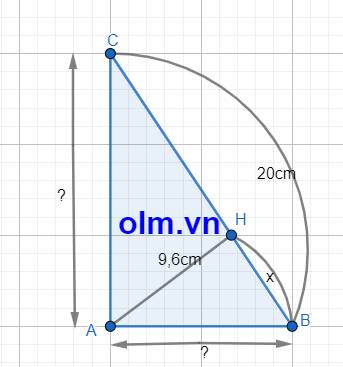
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm
HT
2
\(B=\left(\dfrac{1}{9}-\dfrac{5}{7}\right)+\dfrac{3}{6}+\left(\dfrac{-12}{17}+\dfrac{-1}{2}\right)+\dfrac{5}{9}.\)
\(B=\dfrac{1}{9}-\dfrac{5}{7}+\dfrac{1}{2}-\dfrac{12}{17}-\dfrac{1}{2}+\dfrac{5}{9}.\)
\(B=\left(\dfrac{1}{9}+\dfrac{5}{9}\right)-\dfrac{5}{7}-\dfrac{12}{17}+\left(\dfrac{1}{2}-\dfrac{1}{2}\right).\)
\(B=\dfrac{2}{3}-\dfrac{5}{7}-\dfrac{12}{17}=\dfrac{-269}{357}.\)