cho tam giác ABC có góc A vuông góc, H=60°. Gọi M là trung điểm của AC, kẻ MH vuông góc với BC a)tính góc HMC b)Qua A kẻ 1 đường thẳng song song với đường thẳng BC, cắt đường thẳng MH tại K. Chứng minh MH=MK và AH//CK
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


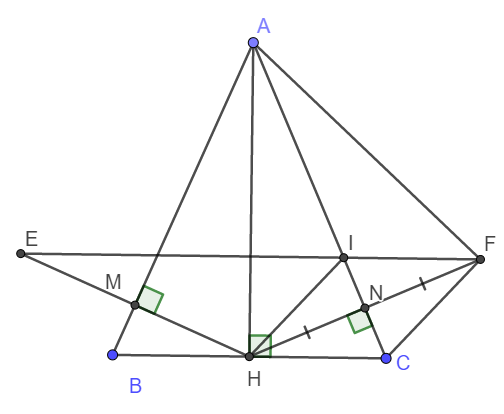
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.

tự kẻ hình nha
a) vì AB=AC=> tam giác ABC cân A=> ABC=ACB=180-90/2=45 độ
xét tam giác ABM và tam giác ACM có
AB=AC(gt)
ABC=ACB(cmt)
BM=CM(gt)
=> tam giác ABM= tam giác ACM(cgc)
b) phải là AM//CK nha
từ tam giác ABM= tam giác ACM=> AMB=AMC(hai góc tương ứng)
mà AMB+AMC=180 độ (kề bù)
=> AMB=AMC=180/2=90 độ=> AM vuông góc với BC, CK vuông góc với BC
=> AM//CK
c) vì tam giác BCK vuông tại C=> CBK+BKC=90 độ=> BKC=90-45=45 độ

a: Xét ΔADE có
AG vừa là đường cao, vừa là phân giác
nên ΔADE cân tại A
=>AD=AE
b: góc BFD=góc DEA
góc BDF=góc BEA
Do đo: góc BFD=góc BDF
=>ΔBFD cân tại B
c: Xét ΔBMF và ΔCME có
góc BMF=góc CME
MB=MC
góc MBF=góc MCE
Do đó: ΔBMF=ΔCME
=>MF=ME
=>M là trung điểm của EF
=>BD=CE
a: \(\widehat{HMC}=30^0\)
b: Xét ΔMHC vuông tại H và ΔMKA vuông tại K có
MC=MA
\(\widehat{CMH}=\widehat{AMK}\)
Do đó: ΔMHC=ΔMKA
Suy ra: MH=MK
Xét tứ giác AHCK có
M là trung điểm của AC
M là trung điểm của HK
Do đó: AHCK là hình bình hành
Suy ra: AH//CK