Tính nguyên...
Đọc tiếp
Tính nguyên hàm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 2 2018
Đáp án D
Với A: Ta có ∫ sin 2 x d x = ∫ 2. sin x . cos x d x = − ∫ 2 cos x d cos x (ta loại A).
Từ A ta xét D luôn có tính chất tương tự.
Với D: Ta có
∫ f x d x = ∫ sin 2 x . d x = ∫ 2 sin x . cos x d x = ∫ 2 sin x d sin x = sin 2 x = g x
Vậy ta chọn D.
CM
28 tháng 8 2018
Chọn B.
Ta phân tích 2 x 2 + 1 = 2 x + 1 2 - 4 x + 1 + 3
Suy ra:
25 tháng 11 2021
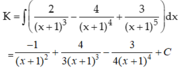
Đặt: \(\left\{{}\begin{matrix}\ln x=u\\\left(x+2\right)dx=dv\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}dx=du\\\dfrac{1}{2}x^2+2x=v\end{matrix}\right.\)
⇒ \(\int\left(x+2\right)\ln xdx=\ln x\left(\dfrac{1}{2}x^2+2x\right)-\int\left(\dfrac{1}{2}x^2+2x\right)\dfrac{1}{x}dx\)
\(=\ln x\left(\dfrac{1}{2}x^2+2x\right)-\dfrac{1}{6}x^3-x^2+C\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2022
\(\int e^x\left(2+\dfrac{e^{-x}}{x}\right)dx=\int\left(2e^x+\dfrac{1}{x}\right)dx=2e^x+ln\left|x\right|+C\)
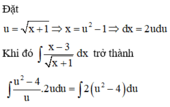
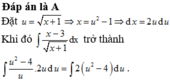
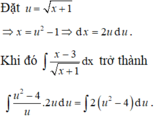
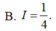
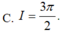
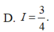
\(I=\int\left(\dfrac{1}{2}+\dfrac{1}{2}cos4x\right)=\dfrac{1}{2}x+\dfrac{1}{8}sin4x+C\)
I=∫(12+12cos4x)=12x+18sin4x+C