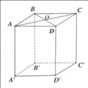
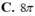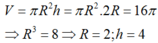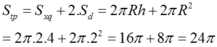Một hình trụ đáy bằng 10 cm và thể tích V=1000 ( cm khối ). tính độ dài đường sinh và diện tích toàn phần của hình trụ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
27 tháng 6 2021
Lời giải:
Khái niệm đường sinh quen thuộc trong hình nón.
Như đề của bạn thì đường sinh chính là đường cao? Thế thì thể tích hình trụ: $\pi r^2h=\pi 3^2.2=18\pi$ (cm khối)
Nhưng mà diện tích xung quanh thì là: $2\pi rh=12\pi$ (cm vuông)
Thể tích và diện tích so sánh với nhau sao được?
31 tháng 7 2023
Gọi đường chéo của hình thoi là d và chu vi đáy là p.
Ta có hệ phương trình sau:
d + d = 24cm (vì đường chéo của hình thoi bằng 24cm)
p = 52cm (vì chu vi đáy của hình thoi bằng 52cm)
Từ đó, ta có:
2d = 24cm
d = 12cm
Vậy đường chéo của hình thoi là 12cm.
Để tính chiều cao của hình lăng trụ, ta sử dụng định lý Pytago:
Chiều cao của hình lăng trụ = căn bậc hai của (d^2 - (cạnh đáy/2)^2)
= căn bậc hai của (12^2 - (10/2)^2)
= căn bậc hai của (144 - 25)
= căn bậc hai của 119
≈ 10.92cm
Vậy chiều cao của hình lăng trụ là khoảng 10.92cm.
Để tính thể tích của hình lăng trụ, ta sử dụng công thức:
Thể tích = diện tích đáy x chiều cao
= (diện tích hình thoi x 2) x chiều cao
= (cạnh đáy x cạnh đáy x sin(góc giữa hai đường chéo) x 2) x chiều cao
= (10cm x 10cm x sin(90°) x 2) x 10.92cm
= (100cm^2 x 1 x 2) x 10.92cm
= 2184cm^3
Vậy thể tích của hình lăng trụ là 2184cm^3
CM
27 tháng 1 2017
Chọn C
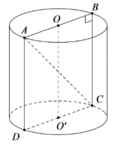
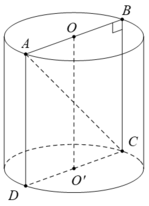
Gọi O,O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD
Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là
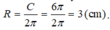
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 cm và AB = 2R = 6cm nên chiều cao của hình trụ là:
CM
11 tháng 8 2018
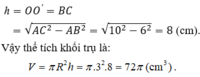
Đáp án C
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6π nên bán kính đáy của hình trụ là
CM
22 tháng 7 2017
Đáp án C
Gọi O, O' là hai tâm của đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6π (cm) nên bán kính đáy của hình trụ là
CM
22 tháng 11 2019
Vì ABCD là hình thoi nên A C ⊥ B D tại trung điểm O của AC và BD (ai đường chéo của hình thoi)
