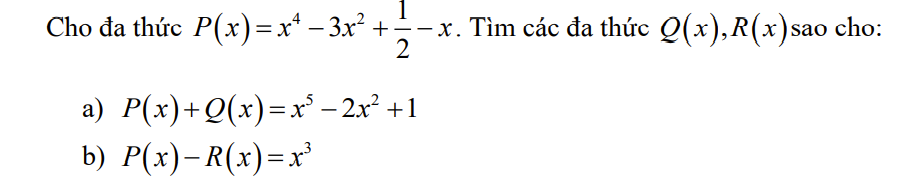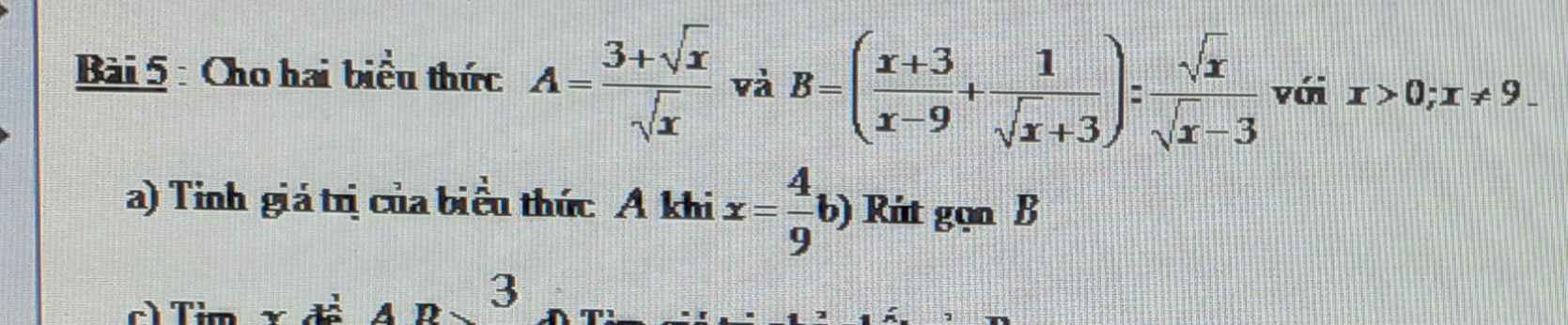câu A thôi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2022
Hiệu điện thế hai đầu cuộn thứ cấp 1 là:
\(\dfrac{U_1}{U_2}=\dfrac{n_1}{n_2}=\dfrac{500}{11000}=\dfrac{1}{22}\)
\(\Rightarrow U_2=22U_1=22\cdot1000=22000V\)
Hiệu điện thế hai đầu cuộn dây thứ cấp 2 là:
\(U_2'=U_2=22000V\)
\(\Rightarrow\dfrac{U_1'}{U_2'}=\dfrac{n_1'}{n_2'}=\dfrac{1320}{132000}=\dfrac{1}{100}\)
\(\Rightarrow U_1'=\dfrac{1}{100}\cdot22000=220V\)
Gửi bạn câu a đó^.^
2
25 tháng 5 2022
`a)P(x)+Q(x)=x^5-2x^2+1`
`=>Q(x)=x^5-2x^2+1-P(x)`
`=>Q(x)=x^5-2x^2+1-x^4+3x^2-1/2+x`
`=>Q(x)=x^5-x^4+x^2+x+1/2`
______________________________________________
`b)P(x)-R(x)=x^3`
`=>R(x)=P(x)-x^3`
`=>R(x)=x^4-3x^2+1/2-x-x^3`
`=>R(x)=x^4-x^3-3x^2-x+1/2`
25 tháng 5 2022
Ta có:
\(P\left(x\right)+Q\left(x\right)=x^5-2x^2+1\)
\(\Rightarrow Q\left(x\right)=P\left(x\right)-\left(x^5-2x^2+1\right)\)
\(=x^4-3x^2+\dfrac{1}{2}-x-x^5+2x^2-1\)
\(=-x^5+x^4-x^2-x-\dfrac{1}{2}\)
Vậy \(Q\left(x\right)=-5^2+x^4-x^2-x-\dfrac{1}{2}\)
11 tháng 8 2021
a) \(\dfrac{\sqrt{15}+\sqrt{21}}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{3}.\sqrt{5}+\sqrt{3}.\sqrt{7}}{\sqrt{5}.\sqrt{7}}=\dfrac{\sqrt{3}\left(\sqrt{5}.\sqrt{7}\right)}{\sqrt{5}.\sqrt{7}}=\sqrt{3}\)
11 tháng 8 2021
a) \(\dfrac{\sqrt{15}+\sqrt{21}}{\sqrt{5}+\sqrt{7}}=\dfrac{\sqrt{3}\left(\sqrt{5}+\sqrt{7}\right)}{\sqrt{5}+\sqrt{7}}=\sqrt{3}\)
T
3
28 tháng 2 2021
b Ta có \(\Lambda ABE=\dfrac{1}{2}sđ\cap BE,\Lambda AFB=\dfrac{1}{2}sđ\cap BE\Rightarrow\Lambda ABE=\Lambda AFB\)
Mà \(\Lambda EAB=\Lambda BAF\) \(\Rightarrow\Delta EAB\sim\Delta BAF\left(g.g\right)\Rightarrow\dfrac{EA}{BA}=\dfrac{AB}{ÀF}\Rightarrow AE\cdot AF=AB^2\left(1\right)\)
Áp dụng hệ thức lượng giác vào \(\Delta AOB\) có:(BH vuông góc với AO)
\(\Rightarrow AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AH\cdot AO=AE\cdot AF\)
28 tháng 2 2021
a) Xét tứ giác ABOC có
\(\widehat{ABO}\) và \(\widehat{ACO}\) là tứ giác nội tiếp
\(\widehat{ABO}+\widehat{ACO}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ABOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét (O) có
\(\widehat{BFE}\) là góc nội tiếp chắn \(\stackrel\frown{BE}\)
\(\widehat{ABE}\) là góc tạo bởi dây cung BE và tiếp tuyến BA
Do đó: \(\widehat{BFE}=\widehat{ABE}\)(Hệ quả góc tạo bởi tiếp tuyến và dây cung)
\(\Leftrightarrow\widehat{BFA}=\widehat{EBA}\)
Xét ΔBFA và ΔEBA có
\(\widehat{BFA}=\widehat{EBA}\)(cmt)
\(\widehat{ABF}\) là góc chung
Do đó: ΔBFA∼ΔEBA(g-g)
\(\Leftrightarrow\dfrac{AF}{AB}=\dfrac{AB}{AE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=AF\cdot AE\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBOA vuông tại B có BH là đường cao ứng với cạnh huyền AO, ta được:
\(AB^2=AH\cdot AO\)(2)
Từ (1) và (2) suy ra \(AF\cdot AE=AH\cdot AO\)(đpcm)
T
1
25 tháng 6 2021
a,theo giả thiết E lần lượt là hình chiếu của H lên AB,
H là chân đường vuông góc kẻ từ B xuống AC
\(=>\)\(\angle\left(BEH\right)=\angle\left(BHA\right)=90^o\)
có \(\angle\left(B\right)chung\)\(=>\Delta BEH\sim\Delta BHA\left(g.g\right)\left(dpcm\right)\)
b, ta có E,F là hình chiếu của H trên AB,BC
\(=>HE\perp AB,HF\perp BC\)
mà \(BH\perp AC\left(gt\right)=>\)\(\Delta BHA\) vuông tại H có HE là đường cao
và \(\Delta BHC\) vuông tại H có HF là đường cao
theo hệ thức lượng
\(=>BH^2=BE.BA=BF.BC\left(dpcm\right)\)
19 tháng 9 2021
\(a,A=\dfrac{3+\sqrt{\dfrac{4}{9}}}{\sqrt{\dfrac{4}{9}}}=\dfrac{3+\dfrac{2}{3}}{\dfrac{2}{3}}=\dfrac{11}{3}:\dfrac{2}{3}=\dfrac{11}{2}\\ b,B=\left(\dfrac{x+3}{x-9}+\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\left(x>0;x\ne9\right)\\ B=\dfrac{x+3+\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}}\\ B=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}+3}\cdot\dfrac{1}{\sqrt{x}}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
19 tháng 9 2021
a)Ta có \(x=\dfrac{4}{9}\Rightarrow\sqrt{x}=\dfrac{2}{3}\)
=>\(A=\dfrac{3+\sqrt{x}}{\sqrt{x}}=\dfrac{3+\dfrac{2}{3}}{\dfrac{2}{3}}=\dfrac{11}{2}\)
Vậy\(A=\dfrac{11}{2}khix=\dfrac{4}{9}\)
b)\(B=\left(\dfrac{x+3}{x-9}+\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(=\dfrac{x+3+\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)
13 tháng 11 2021
a, \(AC=\sqrt{BC^2-AB^2}=16\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=9,6\left(cm\right)\\ \sin ABC=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{ABC}\approx53^0\)
b, Áp dụng HTL: \(AN\cdot AC=AH^2\)
Áp dụng PTG: \(AH^2=AC^2-HC^2\)
Suy ra đpcm
c, Vì \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\) nên AMHN là hcn
Do đó AH=MN
Áp dụng HTL: \(\left\{{}\begin{matrix}AN\cdot NC=HN^2\\AM\cdot MB=HM^2\end{matrix}\right.\)
Áp dụng PTG: \(HN^2+HM^2=MN^2=AH^2\)
Suy ra đpcm