Giải và biện luận phương trình (a và m là các tham số):
a) |2ax + 3 |= 5;
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
Bài 1: Giải và biện luận các phương trình sau theo tham số m a) 2mx + 3 = m - x b) m(x - 2) = 3x + 1
1
6 tháng 12 2021
b: Để phương trình vô nghiệm thì x-2=0
hay x=2
Để phương trình có nghiệm thì x-2<>0
hay x<>2
PT
1
CM
29 tháng 11 2019
Phương trình đã cho tương đương với phương trình
(m - 1)(m + 3)x = 4(m - 1)
Với m ≠ 1 và m ≠ -3 phương trình có nghiệm 
Với m = 1 mọi số thực x đều là nghiệm của phương trình;
Với m = -3 phương trình vô nghiệm.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2021
\(x^2\left(x+2a\right)-\left(a+1\right)^2\left(x+2a\right)=0\)
\(\Leftrightarrow\left(x+2a\right)\left[x^2-\left(a+1\right)^2\right]=0\)
\(\Leftrightarrow\left(x+2a\right)\left(x+a+1\right)\left(x-a-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2a\\x=-a-1\\x=a+1\end{matrix}\right.\)
Pt đã cho luôn có 3 nghiệm (như trên) với mọi a
\(\left\{{}\begin{matrix}-a-1-\left(-2a\right)=a-1< 0\\\left(-a-1\right)-\left(a+1\right)=-2\left(a+1\right)< 0\\\end{matrix}\right.\)
\(\Rightarrow x=-a-1\) là nghiệm nhỏ nhất
PT
1
CM
11 tháng 11 2017
Điều kiện của phương trình là x ≠ -1, ta có
⇒ (m - 2)x + 3 = (2m - 1)(x + 1)
⇒ (m + 1)x = 4 - 2m (1)
Với m = -1 phương trình (1) vô nghiệm nên phương trình đã cho cũng vô nghiệm.
Với m ≠ -1 phương tình (1) có nghiệm 
Nghiệm này thỏa mãn điều kiện x ≠ -1 khi và chỉ khi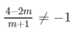 
hay -2m + 4 ≠ -m - 1 ⇒ m ≠ 5
Kết luận
Với m = -1 hoặc m = 5 phương trình vô nghiệm
Với m ≠ -1 và m ≠ 5 phương trình có nghiệm là 
PT
1
CM
8 tháng 9 2017
Điều kiện của phương trình là: x ≠ 3. Ta có:
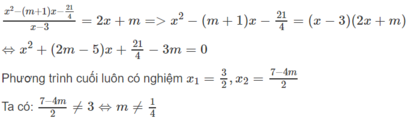
Kết luận
Với m ≠ 1/4 phương trình đã cho có hai nghiệm và x = 3/2 và x = (7 - 4m)/2
Với m ≠ 1/4 phương trình có một nghiệm x = 3/2
PT
1
CM
23 tháng 11 2019
Với m = -1 phương trình đã cho trở thành
-5x + 1 = 0 ⇔ x = 1/5
Với m ≠ -1 phương trình đã cho là một phương trình bậc hai, có biệt thức Δ = -24m + 1
Nếu m ≤ 1/24 thì Δ ≥ 0 phương trình có hai nghiệm
Với m = -1 phương trình có nghiệm là x = 1/5
PT
1
CM
13 tháng 6 2019
Điều kiện của phương trình là x ≠ 1. Khi đó ta có
⇔ (2m + 1)x - m = (x + m)(x - 1)
⇔ x2 - (m + 2)x = 0
⇔ x = 0, x = m + 2
Giá trị x = m + 2 thỏa mãn điều kiện của phương trình khi m ≠ -1
Kết luận
Vậy với m = -1 phương trình có nghiệm duy nhất x = 0;
Với m ≠ -1 phương trình có hai nghiệm x = 0 và x = m + 2.
a) Ta có : |2ax + 3| = 5(1) ⇔ |2ax + 3| = |5| ⇔ 2ax + 3 = 5
hoặc 2ax + 3 = -5 ⇔ 2ax = 2 hoặc 2ax = -8 ⇔ ax = 1 hoặc ax = -4
Nếu a = 0 ⇒ (1) vô nghiệm
Nếu a ≠ 0 ⇒ (1) có hai nghiệm phân biệt : x = 1/a , x = -4/a
b)Điều kiện xác định của phương trình là ∀ x; x ≠ 1 và x ≠ - 1.
Khi đó : (2mx- m2 + m - 2 )/(x2 - 1) = 1 (2)
(2)⇔ 2mx – m2 + m – 2 = x2 – 1 ⇔ x2 – 2mx + m2 – m + 1 = 0 (3)
Ta có : Δ’ = m2 – m2 + m -1 = m – 1
Nếu m – 1 < 0 ⇔ m < 1 ⇒ (3) vô nghiệm ⇒ (2) vô nghiệm
Nếu m – 1 = 0 ⇔ m = 1 ⇒ (3) có nghiệm kép x1 = x2 = 1 ⇒ (2) vô nghiệm
Nếu m - 1 > 0 có m > l =0 (3) có hai nghiệm phân biệt
x1 = m – √(m -1) ; x2 = m + √(m -1) (hiển nhiên x2 > x1)
Vì m > 1 nên x2 > 1 ⇒ x2 luôn là nghiệm của (2). Còn x1 ≤ 1.
Nên : Nếu x1 = -1 ⇔ m – √(m – 1) = - 1 ⇔ m + 1 = √( m – 1)
⇔ m2 + 2m +1 = m – 1(vì m + 1 > 0)
⇔ m2 + m + 2 = 0 phương trình này vô nghiệm tức là x1 ≠ -1 với mọi m > 1.
Vậy x1 = 1 ⇔ m = 2
Tóm lại : m ≤ 1 thì (2) vô nghiệm
m > 1 và m ≠ 2 thì (2) có hai nghiệm phân biệt :
x1 = m – √(m -1) ; x2 = m + √(m -1)
m = 2 thì (2) có một nghiệm x = 3.
Đừng copy nữa em nhé !