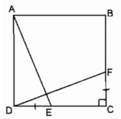
Cho hình vuông ABCD. Trên AB, AD lấy điểm E,F sao cho AE=DF. CMR: DE⊥CF.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ∆ ADE và ∆ DCF:
AD = DC (gt)
∠ A = ∠ D = 90 °
DE = CF (gt)
Do đó: ∆ ADE = ∆ DCF (c.g.c)
⇒ AE = DF
∠ (EAD) = ∠ (FDC)
∠ (EAD) + ∠ (DEA) = 90 ° (vì ΔADE vuông tại A)
⇒ ∠ (FDC) + ∠ (DEA) = 90 °
Gọi I là giao điểm của AE và DF.
Suy ra: ∠ (IDE) + ∠ (DEI) = 90 °
Trong ∆ DEI ta có: ∠ (DIE) = 180 ° – ( ∠ (IDE) + ∠ (DEI) ) = 180 ° – 90 ° = 90 °
Suy ra: AE ⊥ DF

a: Xét ΔAED vuông tại A và ΔDFC vuông tại D có
AD=DC
AE=DF
=>ΔAED=ΔDFC
=>FC=DE
b: Xét tứ giác DQPF có
I là trung điểm chung của DP và QF
DP vuông góc DF
=>DQPF là hình thoi

A B C D E F
\(\Delta ADE=\Delta DCF\left(c-g-c\right)\), suy ra AE = DF và \(\widehat{DAE}=\widehat{CDF}.\)
Ta lại có \(\widehat{CDF}+\widehat{ADF}=90^o\) nên \(\widehat{DAE}+\widehat{ADF}=90^o.\) Do đó
AE \(\perp\) DF.

Gợi í:)
•Chứng minh cho nó bằng 900 (hoặc đường trung tuyến đồng thời là đường phân giác)
-Cái nào bằng 900 vậy bạn :)?