Cho tam giác ABC vuông tại A AB=3cm Ac=4cm vẽ đường cao AE phân giác góc ABC cắt AC tại F tính BF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 5 2023
a: Xét ΔABC vuông tại A và ΔEBA vuông tại E có
góc B chung
=>ΔABC đồng dạng vơi ΔEBA
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
BF là phân giác
=>AF/AB=CF/BC
=>AF/3=CF/5=4/8=0,5
=>AF=1,5cm
\(BF=\sqrt{1,5^2+3^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)
21 tháng 4 2017
Dễ thôi
ta có\(\Delta HBE\infty\Delta ABF\)(\(\widehat{BHE}=\widehat{BAF}=90^0\);\(\widehat{EBH}=\widehat{ABF}\))
\(\Rightarrow\widehat{BEH}=\widehat{AFB}\)
Lại có:\(\widehat{BEH}=\widehat{AEF}\)
\(\Rightarrow\widehat{AFE}=\widehat{AEF}\)
Vậy tam giác AEF cân tại A
TM
24 tháng 4 2021
a, Xét ΔABC có góc BAC vuông
=> \(BC^2=AB^2+AC^2\)
=> \(BC^2=25\)
\(\Rightarrow BC=5\) (cm)
Xét ΔABC và ΔDAC, có
\(\widehat{BAC}=\widehat{ADC}\)
\(\widehat{C}\) chung
=> ΔABC∼ΔDAC(g.g)
=> \(\dfrac{AD}{AB}=\dfrac{AC}{BC}\)
=>\(\dfrac{AD}{3}=\dfrac{4}{5}\)
\(\Rightarrow AD=2,4cm\)
TM
24 tháng 4 2021
b, Vì ΔABC∼ΔDAC (cmt)
=>\(\dfrac{AC}{BA}=\dfrac{DC}{AC}\)
Xét ΔADB và ΔADC, có:
+ \(\widehat{ADC}=\widehat{ADB}\) (=90 độ)
+ \(\dfrac{AC}{BA}=\dfrac{DC}{AC}\)
=> ΔADB∼ΔADC (c.g.c)
=> \(\dfrac{AD}{BD}=\dfrac{DC}{AD}\)
\(\Rightarrow AD.AD=BD.DC\)
=> \(AD^2\)= BD.DC(đpcm)
11 tháng 10 2023
\(BC=\sqrt{3^2+4^2}=5\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{12}{5}cm\)
\(AD=\sqrt{bc\left(1-\left(1-\dfrac{a}{b+C}\right)^2\right)}=\dfrac{4\sqrt{3}}{7}\)
TU
13 tháng 3 2022
+xét tam giác ABC vuông tại A:
=> BC2=AC2+AB2(Định lý pytago)
hay BC2=16+9
BC2= 25
Mà BC>0
=> BC=5(cm)
+xét tam giác ABH vuông tại H và tam giác ABC vuông tại A có:
GÓC B: góc chung
góc A=góc H=90độ (tam giác ABC vuông tại A,AH:đường cao)
=> tam giác ABH đồng dạng với tam giác ABC(góc-góc)
=> BH/AB=BA/BC(các cặp cạnh tương ứng tỉ lệ)
hay BH/3=3/5
=> BH=1,8(cm)
=> HC=5-1,8=4,8(cm)
p/s: mình thấy sai sai , vì sao có dữ liệu phân giác góc C mà lại không dùng đến(bạn tham khảo thử bài mình thôi nhé).Các góc,đồng dạng,độ , bạn cùng kí hiệu.Thông cảm hình mình vẽ hơi tởm=))
13 tháng 9 2023
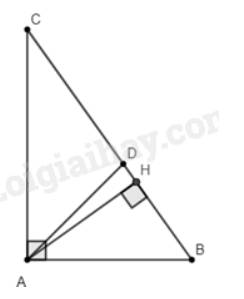
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).
2 tháng 7 2023
a: Xét ΔABC vuông tại A va ΔEBA vuông tại E có
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: BC=căn 6^2+8^2=10cm
BF là phân giác
=>AF/AB=CF/BC
=>AF/3=CF/5=(AF+CF)/(3+5)=8/8=1
=>AF=3cm
BF=căn 6^2+3^2=3*căn 5(cm)