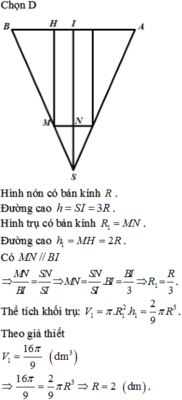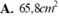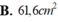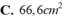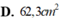Xét bình hình trụ chứa nước được đặt trên mặt phẳng nằm ngang. Bán kính của bình trụ là R, chiều cao mực nước là h, chiều cao bình trụ đủ cao để nước bên trong không bị văng ra ngoài trong toàn bộ quá trình thí nghiệm. Cho cả hệ quay với vận tốc góc ω xung quanh trục của hình trụ. Gia tốc trọng trường là g. Xét mặt phẳng thẳng đứng đi qua trục đối xứng của bình, chọn trục Oy trùng với trục đối xứng của hình trụ, trục Ox nằm trong mặt phẳng và hướng theo phương ngang. Hãy chứng minh mặt thoáng của nước trong mặt phẳng là đường parabol tức có phương trình mô tả dạng hàm bậc hai: y = ax^2 + b. Tìm hệ số a.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

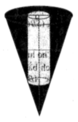
a, đổi \(h1=20cm=0,2m\)
\(S1=100cm^2=0,01m^2\)
\(S2=60cm^2=0,006m^2\)
\(a=1cm=0,01m\)
\(h2=25cm=0,25m\)
khi ở trạng thái cân bằng
\(=>P=Fa\)
\(< =>10m=10Dn.Vc\)
\(< =>10m=10.1000.Sc.hc\)
\(< =>10m=10000.S2.\left(0,2-0,01\right)=10000.0,006.0,19\)
\(=>m=1,14kg\)
\(=>Qtoa\)(nước)\(=1.4200.\left(90-65\right)=105000\left(J\right)\)
\(=>Qthu\)(khối trụ)\(=1,14.2000\left(65-t2\right)\left(J\right)\)
\(=>105000=1,14.2000\left(65-t2\right)=>t2\approx19^oC\)
b, để khối trụ chạm đáy bình khi trong trạng thái cân bằng thì trọng lực của khối trụ và vật đặt thêm phải thằng lực acsimet của nước
\(=>P+Pv\ge Fa1\)
\(< =>10m+10m1\ge\)\(10Dn.Vc\)
\(< =>10.\)\(1,14+10m1\ge10000.0,01.0,25=>m1\ge1,36kg\)
dấu"=" xảy ra<=>m1=1,36kg
=>Khối lượng vật đặt thêm tối thiểu là 1,36kg