Cho tam giác MNP vuông tại M. Đường phân giác NI kẻ IK vuông góc với NP tại K. Cm:
a) MI = IK
b) NI là đường trung trực của MK
c) IP > IM
d) Gọi O là giao điểm của p/g góc MNP và góc MPN. Tính góc NOP
Vẽ hình lun nhaa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
9 tháng 5 2023
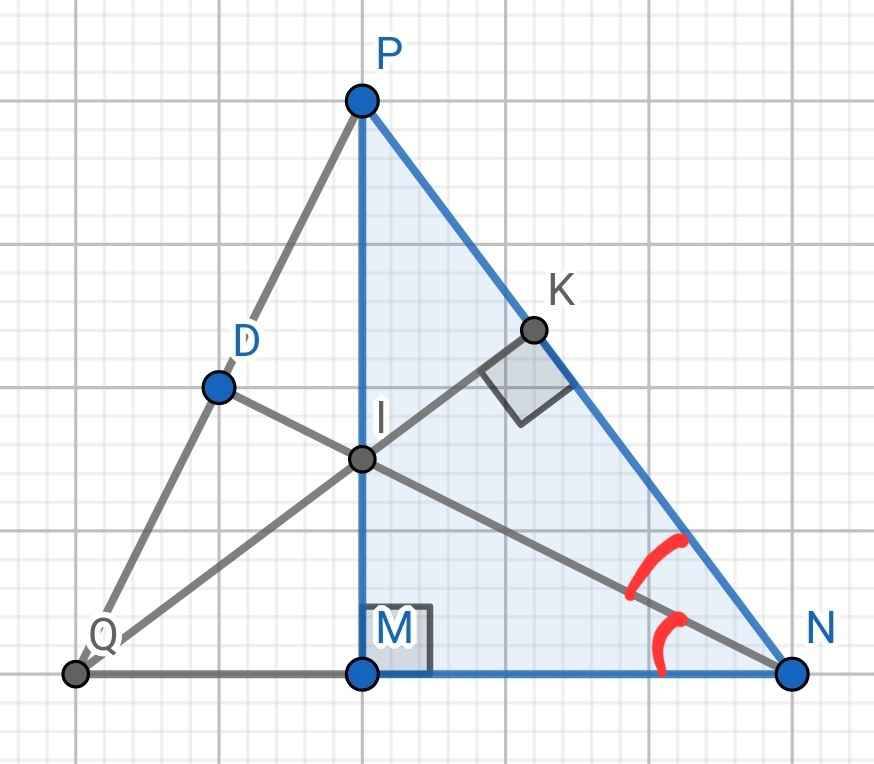
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
30 tháng 4 2023
a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K co
NI chung
góc MNI=góc KNI
=>ΔNMI=ΔNKI
b: Xet ΔIMA vuông tại M và ΔIKP vuông tại K có
IM=IK
góc MIA=góc KIP
=>ΔIMA=ΔIKP
=>KI=IM
=>KI<IA
1 tháng 8 2023
1: Xét ΔMIK vuông tại I và ΔMAK vuông tại A có
MK chung
góc IMK=góc AMK
=>ΔMIK=ΔMAK
=>góc IKM=góc AKM
=>KM là phân giác của góc AKI
2: KI=KA
KA<KP
=>KI<KP
3: Xét ΔMBP có
PI,BA là đường cao
PI cắt BA tại K
=>K là trực tâm
=>MK vuông góc PB
MI=MA
KI=KA
=>MK là trung trực của AI
=>MK vuông góc AI
=>AI//PB
26 tháng 10 2023
a: NP=NI+IP
=5+7=12(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên \(\left\{{}\begin{matrix}MN^2=NI\cdot NP\\MP^2=PK\cdot PN\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}MN=\sqrt{5\cdot12}=2\sqrt{15}\left(cm\right)\\MP=\sqrt{7\cdot12}=2\sqrt{21}\left(cm\right)\end{matrix}\right.\)
b: trung tâm là cái gì vậy bạn?
c: Nếu kẻ như thế thì H trùng với I rồi bạn
Sorry, nhưng bạn tự vẽ hình nha!
a.
Xét tam giác MIN vuông tại M và tam giác KIN vuông tại K có:
NI là cạnh chung
N1 = N2 (Ni là tia phân giác của tam giác MNP)
=> Tam giác MIN = Tam giác KIN (cạnh huyền - góc nhọn)
=> MI = KI (2 cạnh tương ứng)
b.
MI = KI (theo câu a)
NM = NK (tam giác MIN = tam giác KIN)
=> NI là đường trung trực của MK
c.
Tam giác KIP vuông tại K có:
IP > IK (IP là cạnh huyền )
mà IK = IM (theo câu a)
=> IP > IM
d.
Tam giác MNP vuông tại M có:
MPN + MNP = 90
=> MPN = 90 - MNP
MNP = 90 - MPN
OP là tia phân giác của MPN
\(\Rightarrow P1=P2=\frac{MPN}{2}=\frac{90-MNP}{2}\)
ON là tia phân giác của MNP
\(\Rightarrow N1=N2=\frac{MNP}{2}=\frac{90-MPN}{2}\)
Tam giác ONP có:
\(O+P1+N1=180\)
\(O+\frac{90-MNP}{2}+\frac{90-MPN}{2}=180\)
\(O+\frac{90-MNP+90-MPN}{2}=180\)
\(O+\frac{180-\left(MNP+MPN\right)}{2}=180\)
\(O+\frac{180-90}{2}=180\)
\(O+\frac{90}{2}=180\)
\(O+45=180\)
\(O=180-45\)
\(O=135\)