tìm số chẵn dương liên tiếp biết tổng các bình phương của chúng bằng 164
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
T
2
T
1
12 tháng 2 2019
10 và 12 nhé bạn.
---------------------CHÚC BẠN HỌC GIỎI----------------------------------
AH
Akai Haruma
Giáo viên
16 tháng 9 2023
Lời giải:
Gọi số hạng đầu tiên là $a$ và công sai $d$. Khi đó số hạng thứ 2 và 3 lần lượt là $a+d, a+2d$
Theo bài ra ta có:
$a+(a+d)+(a+2d)=12$
$\Rightarrow a+d=4$
$a^2+(a+d)^2+(a+2d)^2=66$
$\Leftrightarrow 3a^2+5d^2+6ad=66$
$\Leftrightarrow 3(4-d)^2+5d^2+6(4-d)d=66$
$\Leftrightarrow 2d^2-18=0$
$\Leftrightarrow d=\pm 3$
Nếu $d=3$ thì $a=1$. Khi đó 3 số cần tìm là $1,4, 7$
Nếu $d=-3$ thì $a=7$. Khi đó 3 số cần tìm là $7, 4, 1$
16 tháng 9 2023
\(S_3=\dfrac{3\left[2u_1+2d\right]}{2}\)
\(\Leftrightarrow2u_1+2d=\dfrac{2S_3}{3}\)
\(\Leftrightarrow2\left(u_1+d\right)=\dfrac{2S_3}{3}\)
\(\Leftrightarrow u_1+d=\dfrac{S_3}{3}=\dfrac{12}{3}=4\)
\(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_2=4\\u_3=7\end{matrix}\right.\)
mà \(u_1^2+u_2^2+u_3^2=1^2+4^2+7^2=66\) (thỏa đề bài)
Vậy 3 số hạng liên tiếp của 1 cấp số cộng là : \(1;4;7\)
9 tháng 7
1.
Đáp số : Các số là : 1884 ; 1882 ; 1880 ; 1888 ; 1890 ; 1892 .
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
9 tháng 7
Bài 1:
Giải:
Trung bình cộng của 7 số chẵn liên tiếp cũng là trung bình cộng của số đầu và số thứ bảy của dãy đó và bằng 18
Tổng của số đầu và số thứ bảy là: 18 x 2 = 36
Hiệu của số thứ nhất và số thứ bảy là: 2 x (7 - 1) = 12
Số thứ nhất là: (36 - 12) : 2 = 12
Số thứ nhất là số chẵn vậy không có 7 số lẻ liên tiếp nào thoả mãn đề bài
19 tháng 7 2016
1) Bài giải :
Đáp số : Sai đề , vì tổng của 3 số lẻ là số lẻ .
2) Bài giải :
Số thứ hai là :
\(2028\div3=676\)
Ba số chẵn liên tiếp có hiệu là 2 .
Vậy số thứ nhất là :
\(676-2=674\)
Số thứ ba là :
\(676+2=678\)
_ Vậy 3 số chẵn liên tiếp đó là : \(674,676,678.\)
Đáp số : Số chẵn thứ nhất : \(674.\)
Số chẵn thứ hai : \(676.\)
Số chẵn thứ ba : \(678.\)
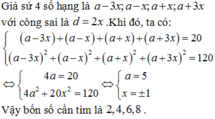
8 và 10 nha
gọi hai số chãn dương liên tiếp là \(a\)và \(a+2\)trong đó \(\left(a>0\right)\)
theo giả thiết thì \(a^2+\left(a+2\right)^2=164\)
<=> \(a^2+a^2+4a+4=164\)
=> \(2a^2+4a-160=0\)
=> \(\left(a-8\right)\left(a+10\right)=0\)=> \(\hept{\begin{cases}a=8\left(tm\right)\\a=-10< 0\left(ktm\right)\end{cases}}\)