vẽ hình và viết gải thiết kết luận giúp mình luôn nha! thank you!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BL
1
Những câu hỏi liên quan
4 tháng 3 2022
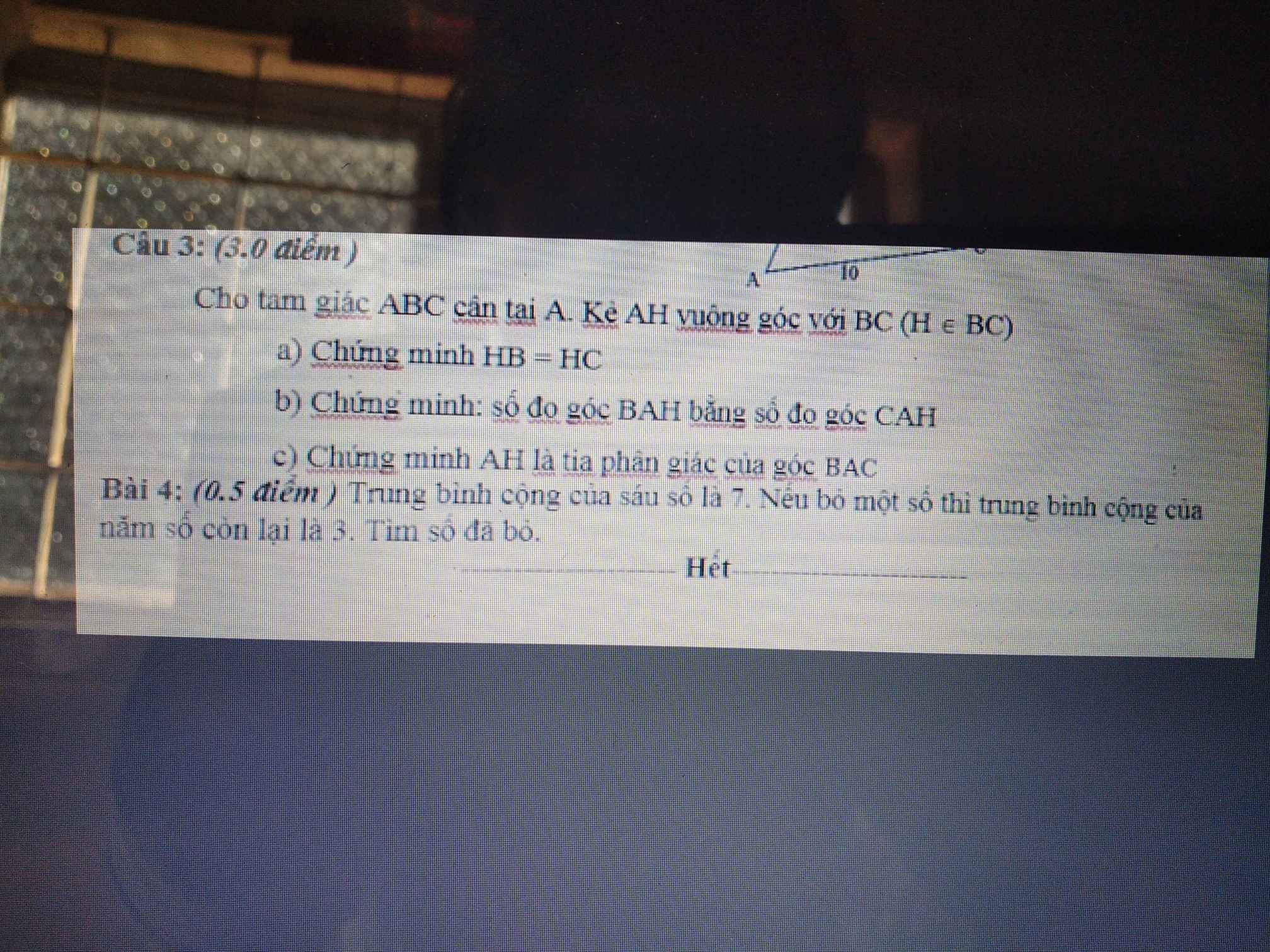
Câu 3:
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra:HB=HC
b: Ta có: ΔAHB=ΔAHC
nên \(\widehat{BAH}=\widehat{CAH}\)
c: Ta có:ΔABC cân tại A
mà AH là đường cao
nên AH là tia phân giác của góc BAC
4 tháng 3 2022
Câu 3:
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH vừa là đường trung tuyến vừa là đường phân giác
=>HB=HC và \(\widehat{BAH}=\widehat{CAH}\)
HN
1
CU
14 tháng 2 2019
a, xét tam giác AMB và tam giác DMB có : MB chung
góc BAC = 90 (gt) = góc MDB do MD _|_ BC (gt)
góc DBM = góc MBA do BM là phân giác của góc ABC (gt)
=> tam giác AMB = tam giác DMB (ch - gn)
=> MA = MD (đn)
b, xét tam giác MEA và tam giác MCD có : MA = MD (Câu a)
Góc AME = góc DMC (đối đỉnh)
góc MAE = góc MDC = 90
=> tam giác MEA = tam giác MCD (cgv - gnk)
=> ME = MC
xét tam giác EMB và tam giác CMB có : BM chung
góc DBM = góc MBA (câu a)
=> tam giác EMB = tam giác CMB (c - g - c)
c, tam giác EMB = tam giác CMB (câu b)
=> BC = BE (đn)
=> tam giác BCE cân tại B (đn)
=> góc CEB = (180 - góc CBE) : 2 (tc) (1)
tam giác AMB = tam giác DMB (Câu a)
=>BD = BA (đn)
=> tam giác BDA cân tại B (đn)
=> góc DAB = (180 - góc CBE) : 2 (tc) (2)
(1)(2) => góc DAB = góc CEB 2 góc này đồng vị
=> AD // EC (tc)
10 tháng 2 2020
Hình vẽ:
Xét \(\Delta AKC\)và \(\Delta AHB\)có:
\(BH=CK\left(gt\right)\)
\(\widehat{A}\)là góc chung
\(\widehat{AKC}=\widehat{AHB}\left(=90^0\right)\)
\(\Rightarrow\Delta AKC=\Delta AHB\left(ch.gn\right)\)
\(\Rightarrow AC=AB\)
\(\Rightarrow\Delta ABC\)cân tại A
Giả thiết: \(\Delta ABC,BH\perp AC\left(H\in AC\right),CK\perp AB\left(K\in AB\right),BH=CK\)
Kết luận: Chứng minh \(\Delta ABC\)cân?
Trả lời hơi muộn, have a nice day!
13 tháng 2 2022
2 người ba đứa bé là bố đứa bé +1 đứa bé =2 người vì ba có thể viết là 3 nhưng tác giả lại cho là ba vậy bí ẩn ở chữ ba
9 tháng 11 2021
a: Giả thiết: a//b
Kết luận: \(\widehat{A_1}=\widehat{B_1}\)
10 tháng 9 2020
Đặt H là giao điểm của Oy và O'x'
Vì Ox//O'x'
=>O1ˆ=H1ˆ( đồng vị)
Vì Oy//O'y'
=>H1ˆ^=O′1ˆ( đồng vị)
Do đó:O1ˆ=O′1ˆ
VậyxOyˆ=x′O′y′ˆ
10 tháng 1 2023
a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |
a: Xét ΔABD và ΔACD có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔABD=ΔACD
b: Ta có: Ay//BC
nên \(\widehat{yAC}=\widehat{ACB}\)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{yAC}=\widehat{ABC}\)