M nằm trong tam giác ABC
Chứng minh: a)MC+MB<AB+AC
b)MA+MB+MC<AB+AC+BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


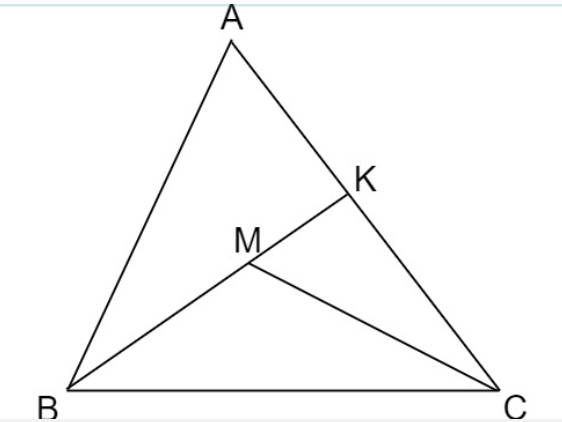
Kéo dài \(BM\) cắt \(AC\) tại \(K\)
Ta có: \(BK< AB+AK\) (bất đẳng thức t/g)
hay \(BM+MK< AB+AK\) \(\left(1\right)\)
Ta lại có: \(MC< MK+KC\) \(\left(2\right)\)
Từ (1) và (2)
\(\Rightarrow BM+MK+MC< AB+AK+MK+KC\)
Hay \(BM+MC< AB+AK+KC\)
Hay \(BM+MC< AB+AC\)
https://lazi.vn/edu/exercise/757051/cho-tam-giac-abc-va-diem-m-nam-trong-tam-giac-chung-minh-rang-mb-mc-ab-ac
`->` Cop giỏi nhỉ?


Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

. M A B C N 1 1 1 2 2 2 2 3 3 1
Trên nửa mặt phẳng bờ AC lấy điểm N sao cho \(\widehat{A}_1=\widehat{A}_2\)và AM=AN
Xét tam giác AMB và tam giác ANC có:
AB=AC(tan giác ABC cân)
\(\widehat{A}_1=\widehat{A}_2\)
AM=AN
=> tam giác AMB= tam giác ANC(c-g-c)
=>\(\widehat{M}_1=\widehat{ANC}\);BM=NC
Mà BM<MC
=>NC<MC
Xét tam giác AMN có AM=AN =>tam giác AMN cân tại A
=>\(\widehat{M}_2=\widehat{N}_2\)(1)
Xét tam giác CNM có NC<MC
=>\(\widehat{M}_3< \widehat{N}_3\)(2)
Từ (1),(2)
=>\(\widehat{M}_2+\widehat{M}_3< \widehat{N}_2+\widehat{N}_3\)
=>\(\widehat{AMC}< \widehat{ANC}\)=>\(\widehat{ANC}>\widehat{AMC}\)
=>\(\widehat{AMB}>\widehat{AMC}\)(\(\widehat{ANC}=\widehat{AMB}\))
Trên nửa mặt phẳng bờ AC lấy điểm N sao cho ˆA1=ˆA2A^1=A^2và AM=AN
Xét tam giác AMB và tam giác ANC có:
AB=AC(tan giác ABC cân)
ˆA1=ˆA2A^1=A^2
AM=AN
=> tam giác AMB= tam giác ANC(c-g-c)
=>ˆM1=ˆANCM^1=ANC^;BM=NC
Mà BM<MC
=>NC<MC
Xét tam giác AMN có AM=AN =>tam giác AMN cân tại A
=>ˆM2=ˆN2M^2=N^2(1)
Xét tam giác CNM có NC<MC
=>ˆM3<ˆN3M^3<N^3(2)
Từ (1),(2)
=>ˆM2+ˆM3<ˆN2+ˆN3M^2+M^3<N^2+N^3
=>ˆAMC<ˆANCAMC^<ANC^=>ˆANC>ˆAMCANC^>AMC^
=>ˆAMB>ˆAMCAMB^>AMC^(ˆANC=ˆAMBANC^=AMB^)

c,Vẽ tam giác đều AMD ( D thuộc nửa mặt phẳng bờ AM không chứa C)(Bạn tự vẽ hình nha, dễ như ăn kẹo ấy)
=> DM = AD = AM
Sau đó bạn chứng minh tam giác ADB = tam giác AMC (c.g.c) (cũng dễ thôi)
=> BD = MC (cặp cạnh tương ứng)
Ta có: DM = AM, BD = MC
=> DM : BM : BD = 3:4:5
=> tam giác BDM vuông tại M
=> góc AMB = 90o + 60o = 150o

Câu hỏi của Nguyễn Hiếu Nhân - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.