Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án cần chọn là: A
+ Nhân cả tử và mẫu của A với 2.4.6.....40 ta được:
A = 1.3.....39 . 2.4.....40 2.4.6.....40 . 21.22.....40 = 1.2.3.....39.40 2.1 . 2.2 . 2.3 ..... 2.20 . 21.22.....40 = 1.2.3.....39.40 2 20 . 1.2.3.....20.21.22.....40 = 1 2 20
+ Nhân cả tử và mẫu của B với 2.4.6.....2n ta được:
B = 1.3..... 2 n − 1 . 2.4.....2 n 2.4.6.....2 n . n + 1 . n + 2 .....2 n = 1.2.3..... 2 n − 1 .2 n 2.1 . 2.2 . 2.3 ..... 2. n . n + 1 . n + 2 .....2 n = 1.2.3..... 2 n − 1 .2 n 2 n . 1.2.3..... n . n + 1 . n + 2 .....2 n = 1 2 n
Vậy A = 1 2 20 , B = 1 2 n

Bài 1:
#include <bits/stdc++.h>
using namespace std;
long long i,n,x,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
if (x%15==0) t=t+x;
}
cout<<t;
return 0;
}

Chọn A.
Ta có: 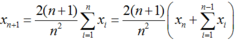
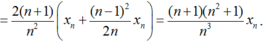
Do đó: 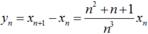
- Ta chứng minh dãy (yn) tăng.
Ta có: 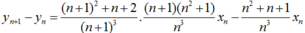
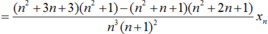
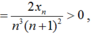
- Ta chứng minh dãy (yn) bị chặn.
Trước hết ta chứng minh: xn ≤ 4(n – 1) (1)
* Với n = 2, ta có: x2 = 4x1 = 4 nên (1) đúng với n = 2
* Giả sử (1) đúng với n, tức là: xn ≤ 4(n – 1), ta có
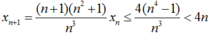
Nên (1) đúng với n + 1. Theo nguyên lí quy nạp ta suy ra (1) đúng
Ta có: 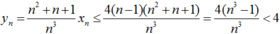
Vậy bài toán được chứng minh.
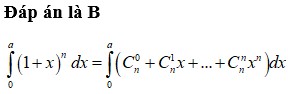
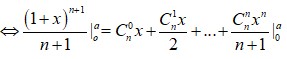
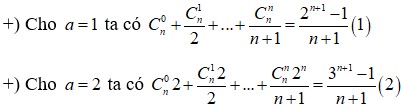

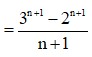
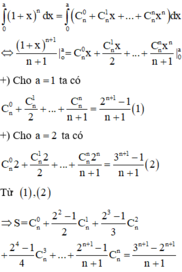
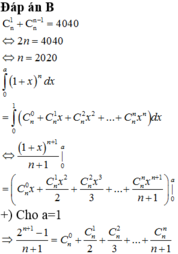
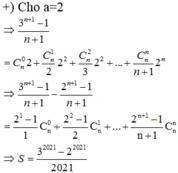
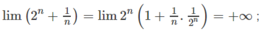
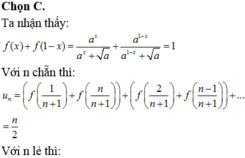
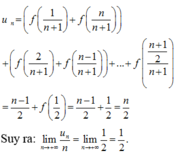
t ui xin nỗi ko biết nàm bài này