cho tam giác ABC vuông ở A.Gọi H là hình chiếu của nđiểm B trên đường phân giác CD của góc C( D thuộc AB).Dựng điểm E sao cho H là trung điểm của DE c/m
a tam giác BED cân
b góc CEB=góc ADC và góc EBH= góc ACD
c, BEvuông góc với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 5 2021
a) Xét ΔBDH vuông tại H và ΔBEH vuông tại H có
BH chung
DH=EH(H là trung điểm của DE)
Do đó: ΔBDH=ΔBEH(hai cạnh góc vuông)
Suy ra: \(\widehat{BDH}=\widehat{BEH}\)(hai góc tương ứng)
mà \(\widehat{BDH}=\widehat{ADC}\)(hai góc đối đỉnh)
và \(\widehat{CEB}=\widehat{BEH}\)
nên \(\widehat{CEB}=\widehat{ADC}\)(đpcm)
Ta có: ΔBDH=ΔBEH(cmt)
nên \(\widehat{DBH}=\widehat{EBH}\)(hai góc tương ứng)(1)
Xét ΔADC vuông tại A và ΔHDB vuông tại H có
\(\widehat{ADC}=\widehat{HDB}\)(hai góc đối đỉnh)
Do đó: ΔADC\(\sim\)ΔHDB(g-g)
Suy ra: \(\widehat{ACD}=\widehat{HBD}\)(hai góc tương ứng)(2)
Từ (1) và (2) suy ra \(\widehat{EBH}=\widehat{ACD}\)(Đpcm)
SN
31 tháng 7 2015
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE
13 tháng 7 2021
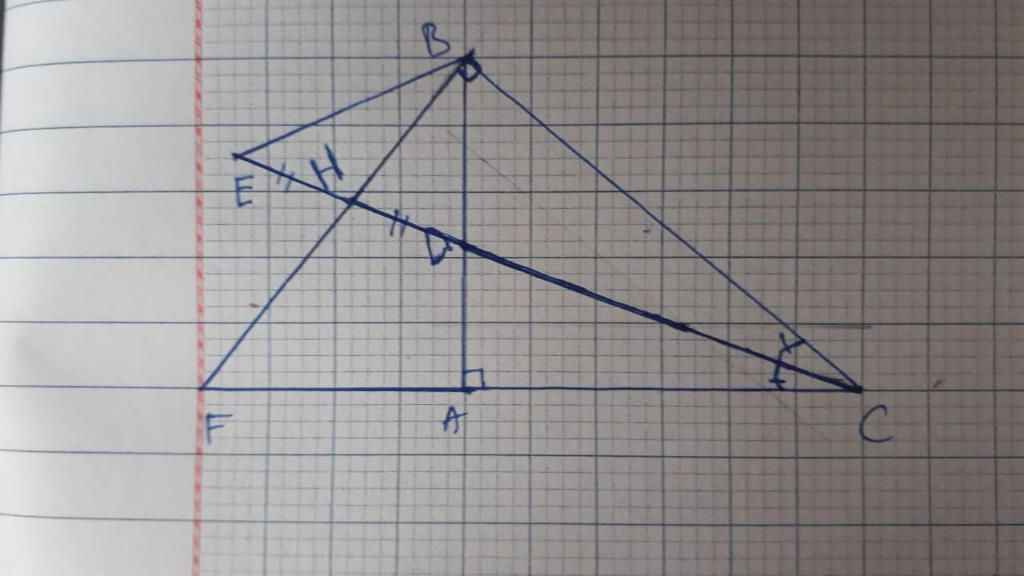
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE