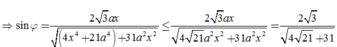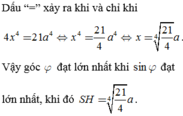cho hình thoi abcd có góc bad=40 độ,o là giao điểm 2 hai đường chéo.gọi h là hình chiếu vuông góc của o trên ab.trên tia đối của tia bc,tia đối của tia dc lần lượt lấy các điểm m,n sao cho hm song song an.tính số đo góc mon
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2022
\(\Delta ADB\text{ cân tại A}\Rightarrow\widehat{ADB}=\dfrac{180^0-\widehat{BAD}}{2}=65^0\\ \text{Ta có }\widehat{MBH}=\widehat{BCD}=\widehat{ADN}=\widehat{BAD}=50^0\\ \Rightarrow\widehat{ODN}=\widehat{ADB}+\widehat{ADN}=115^0\\ MH\text{//}AN\Rightarrow\widehat{MHA}=\widehat{HAN}\\ \Rightarrow\widehat{MHB}+\widehat{MBH}=\widehat{BAD}+\widehat{NAD}\\ \Rightarrow\widehat{MHB}=\widehat{NAD}\\ \Rightarrow\Delta MHB\sim\Delta AND\left(g.g\right)\\ \Rightarrow\dfrac{MB}{AD}=\dfrac{HB}{ND}\Rightarrow MB\cdot NC=AD\cdot HB\left(1\right)\)
\(\left\{{}\begin{matrix}\widehat{OHB}=\widehat{AOD}=90^0\\\widehat{HBO}=\widehat{ODA}\end{matrix}\right.\Rightarrow\Delta HBO\sim\Delta ODA\\ \Rightarrow\dfrac{HB}{OD}=\dfrac{OB}{AD}\Rightarrow HB\cdot AD=OB\cdot OD\left(2\right)\\ \left(1\right)\left(2\right)\Rightarrow\dfrac{MB}{OD}=\dfrac{OB}{ND}\\ \text{Mà }\widehat{MBO}=\widehat{NDO}\\ \Rightarrow\Delta MBO\sim\Delta ODN\left(c.g.c\right)\\ \Rightarrow\widehat{MOB}=\widehat{OND}\Rightarrow\widehat{MOB}+\widehat{NOD}=\widehat{OND}+\widehat{NOD}\\ \Rightarrow\widehat{MOB}+\widehat{NOD}=180^0-\widehat{NDO}=65^0\\ \Rightarrow180^0-\widehat{MON}=65^0\\ \Rightarrow\widehat{MON}=115^0\)
CH
Cô Hoàng Huyền
Admin
VIP
21 tháng 9 2017
a) Do M, N là trung điểm của AB và CD nên MB // DN và MB = CN. Ngoài ta \(MN\perp AB\)
Vậy thì \(\Delta MOB=\Delta NOD\left(g-c-g\right)\Rightarrow OM=ON\)
Lại có HO // AB; \(MN\perp AB\Rightarrow HO\perp MN\)
Xét tam giác HMN có HO là đường cao đồng thời trung tuyến nên nó là tam giác cân, hay HM = HN.
b) Xét tam giác QBP có ON//BP nên \(\frac{QO}{QB}=\frac{QN}{QP}\) (Định lý ta-let)
Xét tam giác MQB có OH//BM nên \(\frac{QO}{QB}=\frac{QH}{QM}\) (Định lý ta-let)
Tức là ta có \(\frac{QH}{QM}=\frac{QN}{QP}\)
Xét tam giác QMP có \(\frac{QH}{QM}=\frac{QN}{QP}\) nên theo định lý Ta let đảo HN // MP.
Vậy thì \(\widehat{HNM}=\widehat{NMP}\) (so le trong)
Lại có do tam giác HMN cân tại H nên \(\widehat{HNM}=\widehat{HMN}\) . Từ đó ta có: \(\widehat{HM}N=\widehat{NMP}\)
hay MN là tian phân giác của \(\widehat{QMP}.\)
CM
29 tháng 1 2018
Đáp án A
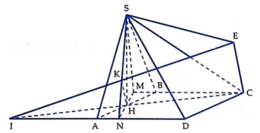
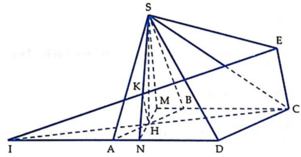
Gọi φ là góc giữa SC và (SAD), N là giao điểm của HM và AD, K là hình chiếu vuông góc của H trên SN, I là giao điểm của HC với AD. Gọi E là điểm đối xứng với I qua K.
Ta có M B = 1 4 B C = a 2 , H B = a , H B M ^ = B A D ^ = 60 °
⇒ H M = H B 2 + M B 2 − 2 H B . M B . c o s H B M ^
⇒ H M = a 2 + a 2 4 − 2 a . a 2 . cos 60 ° = 3 2 a
⇒ H M 2 + M B 2 = 3 2 a 2 + a 2 2 = a 2 = H B 2
⇒ Δ H M B vuông tại M
⇒ H M ⊥ M B hay M N ⊥ B C .
Vì S H ⊥ A D do S H ⊥ A B C D M N ⊥ A D do M N ⊥ B C ⇒ A D ⊥ S M N ⇒ A D ⊥ H K , mà H K ⊥ S N nên H K ⊥ S A D . Lại có HK là đường trung bình của Δ I C E nên H K // C E . Suy ra C E ⊥ S A D tại E và SE là hình chiếu của SC trên mặt phẳng (SAD).
Vậy φ = S C , S A D ^ = S C , S E ^ = C S E ^ .
Đặt S H = x , x > 0 . Do Δ S H N vuông tại H có HK là đường cao nên ta có
1 H K 2 = 1 S H 2 + 1 H N 2 ⇒ H K = S H . H N S H 2 + H N 2 = 3 a x 4 x 2 + 3 a 2 ⇒ C E = 2 H K = 2 3 a x 4 x 2 + 3 a 2
Do Δ S H C vuông tại H nên
S C = S H 2 + H C 2 = S H 2 + H M 2 + M C 2 = x 2 + 3 2 a 2 + 5 a 2 2 = x 2 + 7 a 2
Δ S E C vuông tại E nên sin φ = sin C S E ^ = E C S C = 2 3 a x 4 x 2 + 3 a 2 x 2 + 7 a 2
⇒ sin φ = 2 3 a x 4 x 4 + 21 a 4 + 31 a 2 x 2 ≤ 2 3 a x 4 21 a 2 x 2 + 31 a 2 x 2 = 2 3 4 21 + 31
Dấu “=” xảy ra khi và chỉ khi 4 x 4 = 21 a 4 ⇔ x 4 = 21 4 a 4 ⇔ x = 21 4 4 a .
Vậy góc φ đạt lớn nhất khi sin φ đạt lớn nhất, khi đó S H = 21 4 4 a
