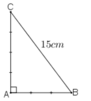
cho tam giác ABC vuông tại A có AB/AC = 3/4 và BC = 15cm. Tính các độ dài AB, AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 9 2019
Theo đề bài ta có:
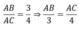
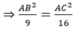
Theo tính chất dãy tỉ số bằng mhau ta có:
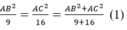
tam giác ABC vuông tại A
Áp dụng định lí pitago vào tam giác ABC ta có:
BC2 = AB2 + AC2 (2)
Từ (1) và (2) suy ra:
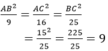
AB2 = 9. 9 = 81 ⇒ AB = 9 cm (vì AB > 0)
AC2 = 16. 9 = 144 ⇒ AC = 12 cm (vì AC > 0)
29 tháng 4 2020
Mình làm mẫu cho bạn câu a) nhé
a) Theo định lí Pytago ta có :
BC2 = AB2 + AC2
152 = AB2 + AC2
AB : AC = 3:4
=> \(\frac{AB}{3}=\frac{AC}{4}\)=> \(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}\)và AB2 + AC2 = 152
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{AB^2}{3^2}=\frac{AC^2}{4^2}=\frac{AB^2+AC^2}{3^2+4^2}=\frac{15^2}{25}=\frac{225}{25}=9\)
\(\frac{AB^2}{3^2}=9\Rightarrow AB^2=81\Rightarrow AB=\sqrt{81}=9cm\)
\(\frac{AC^2}{4^2}=9\Rightarrow AC^2=144\Rightarrow AC=\sqrt{144}=12cm\)
Ý b) tương tự nhé
17 tháng 9 2021
Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC=12\left(cm\right)\)
\(\Leftrightarrow AB=9\left(cm\right)\)
hay AH=7,2(cm)
CM
3 tháng 4 2019
Ta có AB : AC = 3 : 4 ⇔ A B 3 = A C 4 ⇒ A B 2 9 = A C 2 16
= A B 2 + A C 2 9 + 16 = A B 2 + A C 2 25 = B C 2 25 = 225 25 = 9
(Vì theo định lý Py-ta-go ta có A B 2 + A C 2 = B C 2 ⇔ A B 2 + A C 2 = 225 )
Nên A B 2 9 = 9 ⇒ AB = 9; A C 2 9 = 9 ⇒ AC = 12
Theo hệ thức lượng trong tam giác vuông ABC ta có:
A B 2 = B H . B C ⇒ B H = A B 2 B C = 81 15 = 5 , 4
Vậy BH = 5,4
Đáp án cần chọn là: A
30 tháng 9 2021
bài 9
tam giác ABC vuông tại A có
* BC2=AB2+AC2
BC2=152+202=625
BC=25cm
* AH.BC=AB.AC
AH.25=15.20
AH.25=300
AH=12cm
30 tháng 9 2021
tam giác ABH vuông tại H có
BH2=AB2-AH2
BH2=152-122=81
BH=9cm
tam giác ABC vuông tại A có
*AB2=BH.BC
225=9.BC
BC=25cm
CH=BC-BH=25-9=16cm
*AC2=BC2-AB2
AC2=252-152=400
AC=20cm
28 tháng 8 2021
Ta có : \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Theo định lí Pytago tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow\left(\frac{3}{4}AC\right)^2+AC^2=225\Rightarrow AC=12\)cm
\(\Rightarrow AB=\frac{3}{4}AC=\frac{3}{4}.12=9\)cm
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thúc : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{81}{15}=\frac{27}{5}\)cm
\(\Rightarrow CH=BC-BH=15-\frac{27}{5}=\frac{48}{5}\)cm