giải nhanh giúp mình nhé !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Ta có : abcdeg= 1000abc + deg = 1001abc + ( abc - deg )
mà 1001 chia hết cho 13 vá abc -deg cung chia hết cho 13
=>abcdeg chia hết cho 13

Bài 3:
Nhà trường có thể chia đều được, vì 42 chia hết cho 3

\(\dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+\dfrac{1}{4\times5}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}\)
\(=1-\dfrac{1}{5}\)
\(=\dfrac{4}{5}\)

a. Ta có: \(\hat{AOA_1}=2^o,\hat{AOA_2}=4^o,...\Rightarrow\hat{AOA_{50}}=100^o\)
Mà \(\hat{AOB}\) là góc bẹt \(\Rightarrow\hat{AOB}=180^o\)
\(\Rightarrow\hat{A_{50}OB}=\hat{AOB}-\hat{AOA_{50}}=180^o-100^o=80^o\)
- Mặt khác: \(\hat{BOB_1}=1^o,\hat{BOB_2}=3^o,...\Rightarrow\hat{BOB_{50}}=99^o\)
Tương tự như trên: \(\Rightarrow\hat{AOB_{50}}=\hat{AOB}-\hat{BOB_{50}}=180^o-99^o=81^o\)
- Từ đó suy ra: \(\hat{A_{50}OB_{50}}=\hat{AOB}-\hat{AOB_{50}}-\hat{A_{50}OB}=180^o-81^o-80^o=19^o\)
b. Dựa vào a. ta suy ra được công thức sau:
\(\hat{A_nOB_m}=\hat{AOB}-\left(\hat{AOB}-\hat{AOA_n}\right)-\left(\hat{AOB}-\hat{BOB_m}\right)\)
\(=\hat{AOB}-\hat{A_nOB}-\hat{AOB_m}\)

10% của 2 000 công nhân là :
2 000 x 10% = 200 ( nhân viên )
Sau 3 năm nhà máy đó có tất cả số công nhân là :
2 000 + 200 x 3 = 2 600 ( nhân viên )
đ/s :..


Bài 2:
Tử số của phân số ban đầu là 12 nên x cộng vào tử số tức là: \(x+12\)
Mẫu số của phân số ban đầu là 17 nên x cộng vào mẫu tức là: \(x+17\)
Phân số mới có dạng: \(\dfrac{x+12}{x+17}\)
Mà phân số này bằng phân số \(\dfrac{14}{19}\) nên:
\(\dfrac{x+12}{x+17}=\dfrac{14}{19}\)
\(19\times\left(x+12\right)=14\times\left(x+17\right)\)
\(19\times x+228=14\times x+238\)
\(19\times x-14\times x=238-228\)
\(5\times x=10\)
\(x=10:5\)
\(x=2\)
Vậy: ...

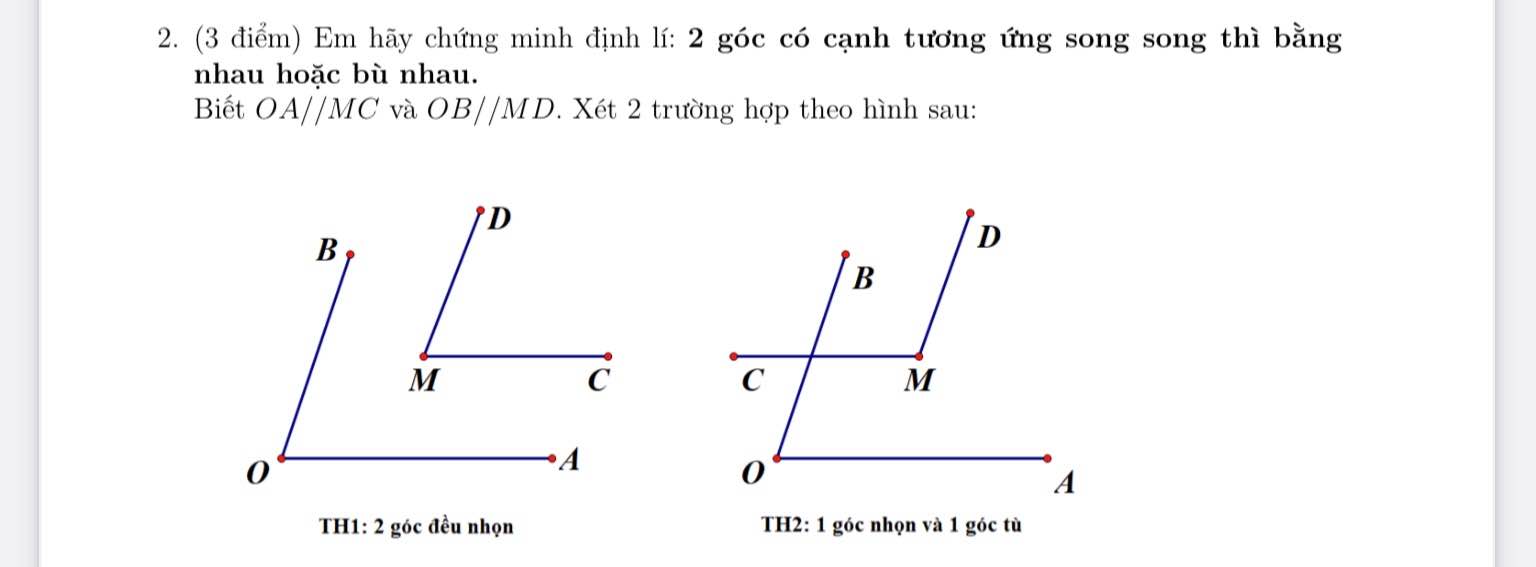

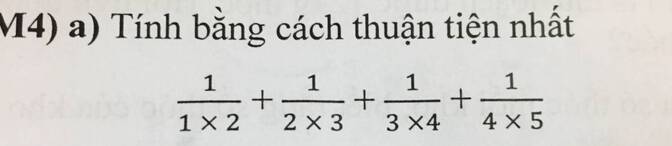 Giúp mình bài này được không?
Giúp mình bài này được không? 



Tỉ số ghế ở phòng thứ hai và phòng thứ nhất là:
\(1\div\frac{5}{4}=\frac{4}{5}\)
Tỉ số ghế ở phòng thứ hai sau khi thêm ghế và phòng thứ nhất là:
\(1\div\frac{10}{9}=\frac{9}{10}\)
Số ghế ở phòng thứ nhất lúc đầu là:
\(2\div\left(\frac{9}{10}-\frac{4}{5}\right)=20\)(cái)
Số ghế ở phòng thứ hai lúc đầu là:
\(20\times\frac{4}{5}=16\)(cái)