giải chi tiết giúp mình ah
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giải chi tiết giúp mình ah
14 tháng 1 2022
Bài 45:
a: Số thứ nhất là: 90:15x7=42
Số thứ hai là 90-42=48
b: Số thứ nhất là 33:3x8=88
Số thứ hai là 88-33=55
Bài 46:
Số cây chanh là:
64:4x3=48(cây)
DT
28 tháng 12 2021
\(\dfrac{1-2x+3+2y+2x-4}{6xy}=\dfrac{2y}{6xy}=\dfrac{1}{3x}\)
\(\dfrac{3+2x-3-4x}{6x}=\dfrac{-2x}{6x}=-\dfrac{1}{3}\)
\(\dfrac{\left(1-2x\right)2xy}{6xy.3.\left(1-2x\right)}=\dfrac{2xy}{18xy}=\dfrac{1}{9}\)
chi tiết rùi k ghi lại đề thui
giải chi tiết giúp mk ah
N
14 tháng 1 2022
Lời giải:
a) Nửa chu vi của sân vận động đó hay tổng chiều dài và chiều rộng của sân vận động hình chữ nhật là:
400 : 2 = 200 (m)
Do chiều dài bằng 3232 chiều rộng. Nên coi chiều rộng sân vận động là 2 phần thì chiều dài sân vận động là 3 phần bằng nhau như thế. Ta có sơ đồ như hình vẽ:
Chiều dài: |-----|-----|-----|
Chiều rộng: |-----|-----|
Chiều rộng của sân vận động đó là:
200:(2+3)x2=80 (m)
Chiều dài của sân vận động đó là:
200-80=120 (m)
b) Diện tích của sân vận động đó là:
120x80=9600 (m²)
Đáp án: a) 120m, 80m
b) 9600m²
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 6 2023
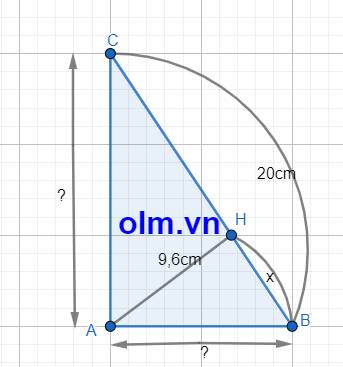
Gọi độ dài đoạn BH là: \(x\) ( cm) ; \(x\) > 0; AC > AB nên \(x\) < CH
Xét tam giác vuông HAB vuông tại H theo pytago ta có:
AB2 = HA2 + HB2 = 9,62 + \(x^2\) = 92,16 + \(x^2\)
Xét tam giác vuông AHC vuông tại H theo pytago ta có:
AC2 = HA2 + HC2 = 9,62 + (\(20-x\))2 = 92,16 + 400 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(x\) + \(x^2\)
Xét tam giác vuông ABC vuông tại A theo pytago ta có:
AC2 + AB2 = BC2
492,16 - 40\(x\) + \(x^2\) + 92,16 + \(x^2\) = 202
(\(x^2\) + \(x^2\)) - 40\(x\) + (492,16 + 92,16) - 400 = 0
2\(x^2\) - 40\(x\) + 584,32 - 400 = 0
2\(x^2\)- 40\(x\) + 184,32 =0
\(x^2\) - 20\(x\) + 92,16 = 0
△' = 102 - 92,16 = 7,84 > 0
\(x\)1 = -(-10) + \(\sqrt{7,84}\) = 12,8 ⇒ CH = 20 - 12,8 = 7,2 < BH (loại )
\(x_2\) = -(-10) - \(\sqrt{7,84}\) = 7,2 ⇒ CH = 20 - 7,2 = 12,8 (thỏa mãn)
Thay \(x_2\) = 7,2 vào biểu thức: AB2 = 92,16 + \(x^2\) = 92,16 + 7,22 = 144
⇒AB = \(\sqrt{144}\) = 12
Thay \(x_2\) = 7,2 vào biểu thức: AC2 = 492,16 - 40\(x\) + \(x^2\)
AC2 = 492,16 - 40\(\times\) 7,2 + 7,22 = 256
AC = \(\sqrt{256}\) = 16
Kết luận AB = 12 cm; AC = 16 cm
L
13 tháng 7 2021
a) Áp dụng định lí Pytago trong \(\Delta\) AHC vuông tại H ta có :
\(AH^2+HC^2=AC^2\)
\(\Rightarrow HC^2=AC^2-AH^2\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}=\sqrt{40^2-24^2}=32cm\)
b) Áp dụng định lí Pytago trong \(\Delta\) AHC vuông tại H ta có :
\(AH^2+HC^2=AC^2\)
\(\Rightarrow AC=\sqrt{AH^2+HC^2}=\sqrt{9,6^2+12,8^2}=16cm\)
AT
13 tháng 7 2021
c) \(BC=CH+BH=72+12,5=84,5\left(cm\right)\)
Ta có: \(\left\{{}\begin{matrix}AB^2=BH.BC=12,5.84,5=1056,25\\AC^2=CH.BC=72.84,5=6084\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{65}{2}\left(cm\right)\\AC=78\left(cm\right)\end{matrix}\right.\)
Ta có: \(AB.AC=AH.BC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{78.\dfrac{65}{2}}{84,5}=30\left(cm\right)\)
B1
30 tháng 7 2017
1) Ta có BC = BD + DC = 15 + 20 = 35cm
AB / AC = BD / DC = 15 / 20 = 3/4
<=> AB = 3/4.AC
Áp dụng Pytago :
AB² + AC² = 35²
<=> (3/4AC)² + AC² = 35²
<=> 0,5625AC² + AC² = 35²
<=> 1,5625AC² = 35²
<=> AC² = 35² / 1,5625 = 784
<=> AC = 28 cm
=> AB = 3/4 . 28 =21 cm
Cos C = 21 / 35 = 3/5
AD² = AC² + DC² - 2.AC.DC.cosC
<=> AD² = 28² + 20² - 2.28.20.3/5
<=> AD = 16√2 cm = 22,63 cm
quá dễ dàng
động não đi
45
a)
Tổng số phần bằng nhau:
7+8=15(phần)
Số bé:
90:15x7=42
Số lớn :
90-42=48
b)
Hiệu số phần bằng nhau:
8-5=3(phần)
Số bé:
33:3x5=55
Số lớn:
33:3x8=88
45.
Số thứ nhất là:
90 : (7+8) x 7= 42
Số thứ hai là:
90 : (7+8) x 8 = 48
Đáp số: Số thứ Nhất: 42
Số thứ Hai: 48
46.
Số thứ Nhất là:
33: (8 - 5) x 8 = 88
Số thứ Hai Là:
88-33 = 55
Đáp số: Số thứ nhất: 88
Số thứ hai: 55