Chứng minh đẳng thức
-[19-2x]+39=2x+20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\text{a/-(59-3x)+39 = 3x -20}\)
\(-59+3x+39=3x-20\)
\(3x-59+39=3x-20\)
\(3x-20=3x-20\)
\(\Leftrightarrowđpcm\)
\(\text{b/ -(a+b+c) +(b-c) - (a-c-1)= 1+c- 2a }\)
\(-a-b-c+b-c-a+c+1=1+c-2a\)
\(1+\left(-b+b\right)+\left(-c-c+c\right)+\left(-a-a\right)=1+c-2a\)
\(1+0-c-2a=1+c-2a\)
\(1-c-2a=1+c-2a\)
\(\Rightarrow\)không thỏa mãn đề bàii
\(\text{c/ -(19-2x)=39= 2x+20}\)
\(-19+2x+39=2x+20\)
\(2x+\left(-19+39\right)=2x+20\)
\(2x+20=2x+20\)
\(\Leftrightarrowđpcm\)
\(\text{d/ b/ -(a+b+c) +(b-c) - (a-c+1)= c-2a-1 }\)
\(-a-b-c+b-c-a+c-1=c-2a-1\)
\(\left(-b+b\right)+\left(-c-c+c\right)+\left(-a-a\right)-1=c-2a-1\)
\(0-c-2a-1=c-2a-1\)
\(-c-2a-1=c-2a-1\)
\(\Leftrightarrow ko\)thỏa mãn đề bài
chúc bạn học tốt

Ta có: \(2x^2+2x+1\)
\(=2\left(x^2+x+\frac{1}{2}\right)\)
\(=2\left(x^2+2\cdot x\cdot\frac{1}{2}+\frac{1}{4}+\frac{1}{4}\right)\)
\(=2\left(x+\frac{1}{2}\right)^2+\frac{1}{2}\)
Ta có: \(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x+\frac{1}{2}\right)^2+\frac{1}{2}\ge\frac{1}{2}\forall x\)
hay \(2x^2+2x+1>0\forall x\)(đpcm)
Này giải chi tiết cho mk cái bước 3 và 4 đi Nguyễn Lê Phước Thịnh

Chứng minh đẳng thức:

Biến đổi vế trái (VT), ta có: MTC = x2 – 4.
4
x
x
2
-
4
+
x
x
+
2
+
2
x
-
2
=
x
+
2
x
-
2
![]()
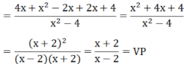
\(\text{VT=- 19+2x+39= 2x+20}\)
\(VT=-19 + 2x + 39 = 2x + 20\)